MATH 410 Midterm: MATH410_BOYLE-M_FALL1996_0101_MID_EXAM_2

• School: University of Maryland
• Department: Mathematics
• Course: MATH 410
• Professor: All

Document Summary

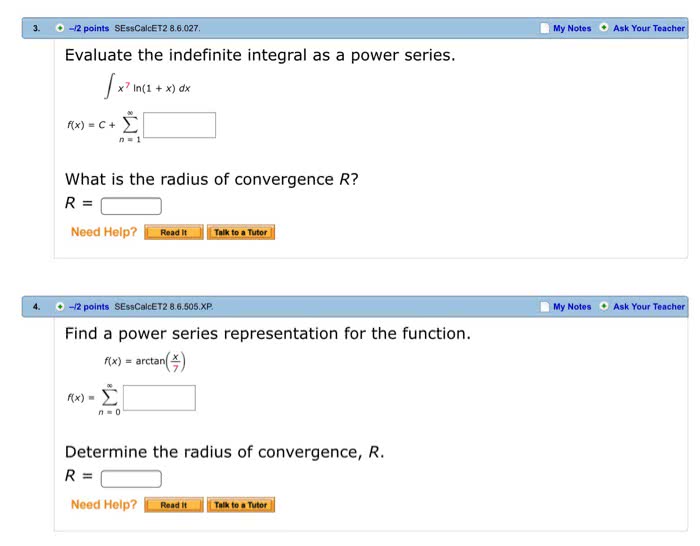
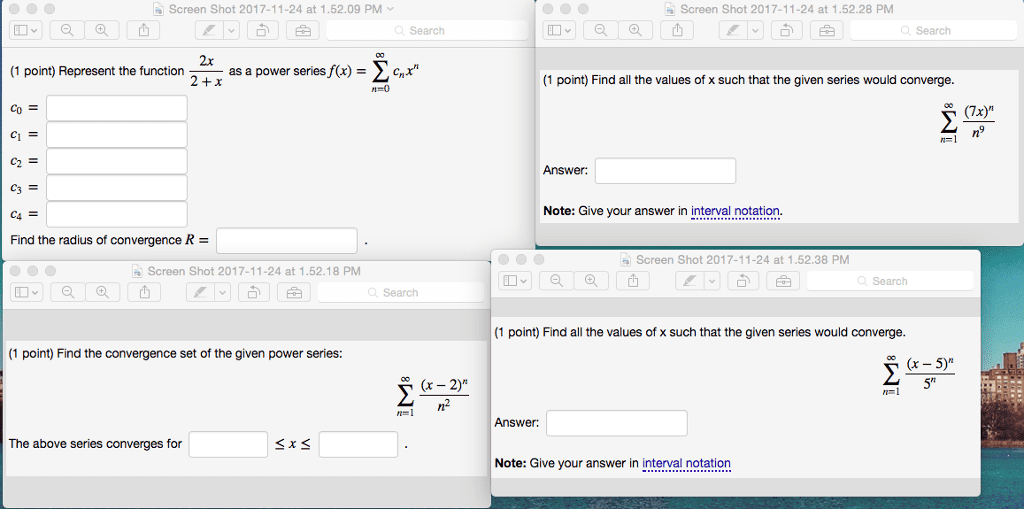
Each problem below is worth 20 points: let pn denote the nth taylor polynomial for the function f (x) = cos(2x). 1 (n + 1): determine which of the following series converge. 1 n: de ne functions fn: [3, ) r by the rules fn(x) = 1/(nx). Prove that {fn} converges uniformly to 0: suppose a sequence of continuous functions fn : d r converges uniformly to a function f . Prove f is continuous: for each part, write true or false (no explanation required).