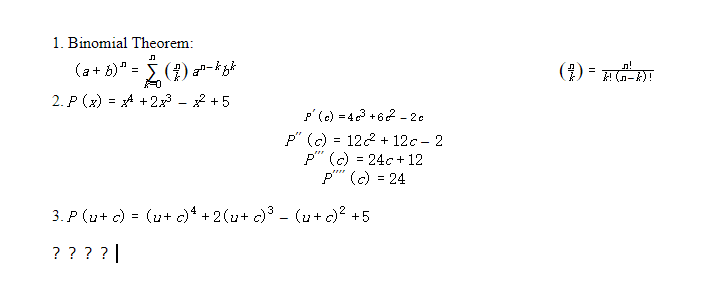MATH 416 Final: MATH416 BOYLE-M SPRING2015 0101 FINAL SOL

• School: University of Maryland
• Department: Mathematics
• Course: MATH 416
• Professor: All

Document Summary

Math 416 spring 2015 final exam: (4 pts) write x3 as a linear combination of chebyshev polynomials. Using t0(x) = 1 and t1(x) = x and then the recursion relation tn(x) = 2xtn 1(x) tn 2(x), we have t2(x) = 2x2 1 and t3(x) = 2x(2x2 1) x = 4x3 3x. So, x3 = (1/4)t3(x) + (3/4)t1(x) : (4 pts) write a polynomial p(x) of degree 3 or less such that p(2) = 1 and p(3) = p(4) = p(5) = 0. 2(cid:18)1 i i (cid:19) = 1 2 i 2 i 2! 1 p(x) = (x 3)(x 4)(x 5) (2 3)(2 4)(2 5: (6 pts) for n 1, de ne cn(t) = 2 cos(2 nt), sn(t) = 2 sin(2 nt) and en(t) = e2 int. Find the matrix u such that for every positive integer n the following holds: then acn + bsn = en + e n .