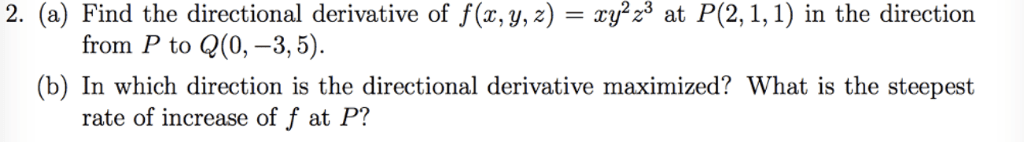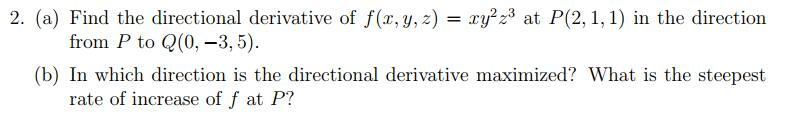MATH 210 Study Guide - Final Guide: Gradient Descent, Directional Derivative, Unit Vector
Document Summary
Problem 1 solution: let f (x, y) = y cos(x2y). Compute the directional derivative at p = (0, 0) in the direction. Find the direction of the steepest descent at p . Solution: by de nition, the directional derivative of f (x, y) at the point (a, b) in the direc- tion of the unit vector u is given by the formula. F (x, y) = hfx, fyi = (cid:10) 2xy2 sin(x2y), cos(x2y) x2y sin(x2y)(cid:11) At the point p = (0, 0) we have. The direction of steepest descent for f (x, y) at (a, b) is. D uf (0, 0) = h0, 1i h0, 1i = 1. F (a, b)(cid:12)(cid:12) (cid:12) (cid:12)(cid:12)(cid:12) (cid:12)(cid:12) (cid:12) (cid:12)(cid:12) (cid:12) Thus, at the point (0, 0) the direction of steepest descent is. Problem 4 solution: find and classify all local extrema of the function f (x, y) = xyey x on the plane.