MATH 1372 Midterm: MATH 1372 UMN midterm3PracticeAnswers
94 views6 pages
Document Summary
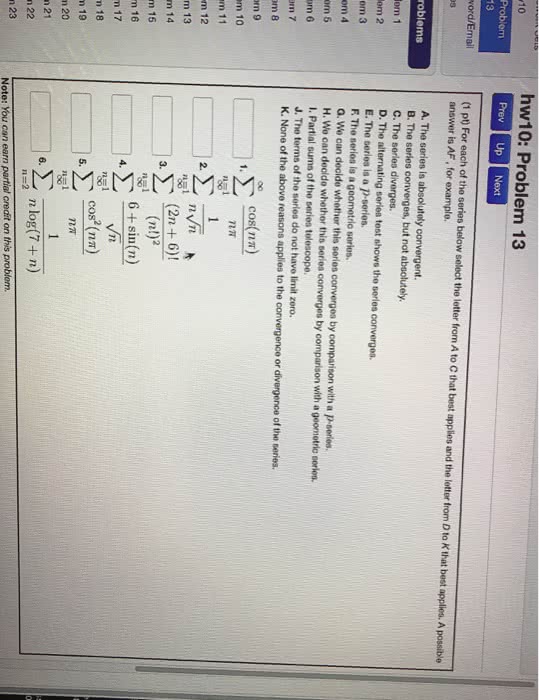
Answers: we have one theorem whose conclusion says an alternating series converges. We have another theorem whose conclusion says an alternating series diverges. Answer: the alternating series theorem says that for the alternating. The divergence theorem for alternating series says that for the alter- ( 1)n 1 3n + 7. 2n2+8 = l and l 6= 0, then series. 2n2 + 8 (3n + 10)(2n2 + 8) < (3n + 7)(2(n + 1)2 + 8) 6n3 + 20n2 + 24n + 80 < (3n + 7)(2n2 + 4n + 10) 6n3 + 20n2 + 24n + 80 < 6n3 + 29n2 + 58n + 70. Since 10 < 9n2 + 34n is clearly true for n 1, we conclude that (2) is true. converges. Since (1) and (2) are true, we conclude that. Justify your bn = 3n+7 answer to the question using this statement. Answer: the divergence theorem for alternating series says that if limn .