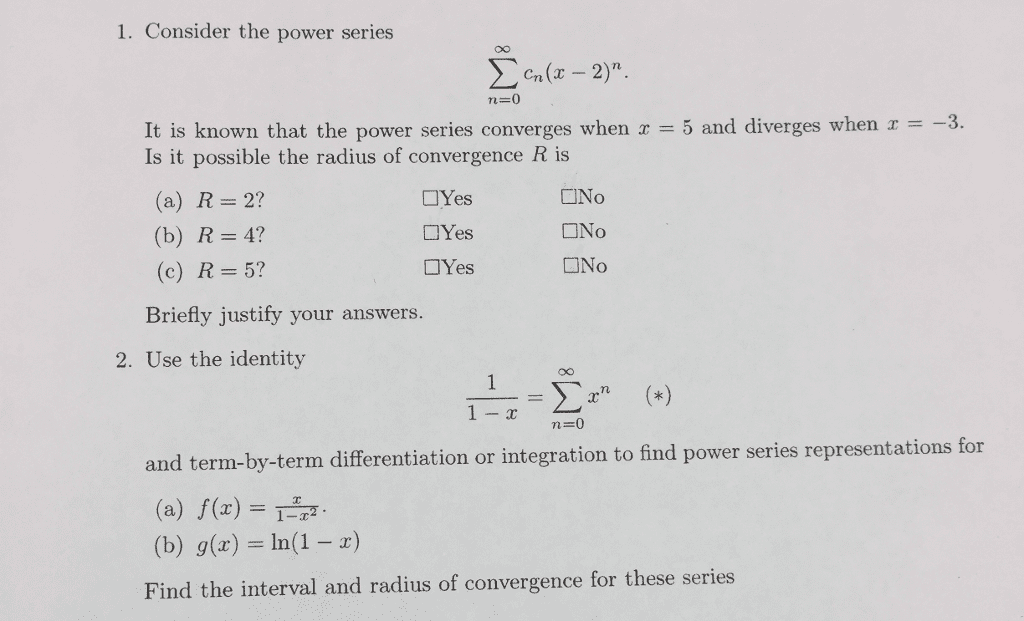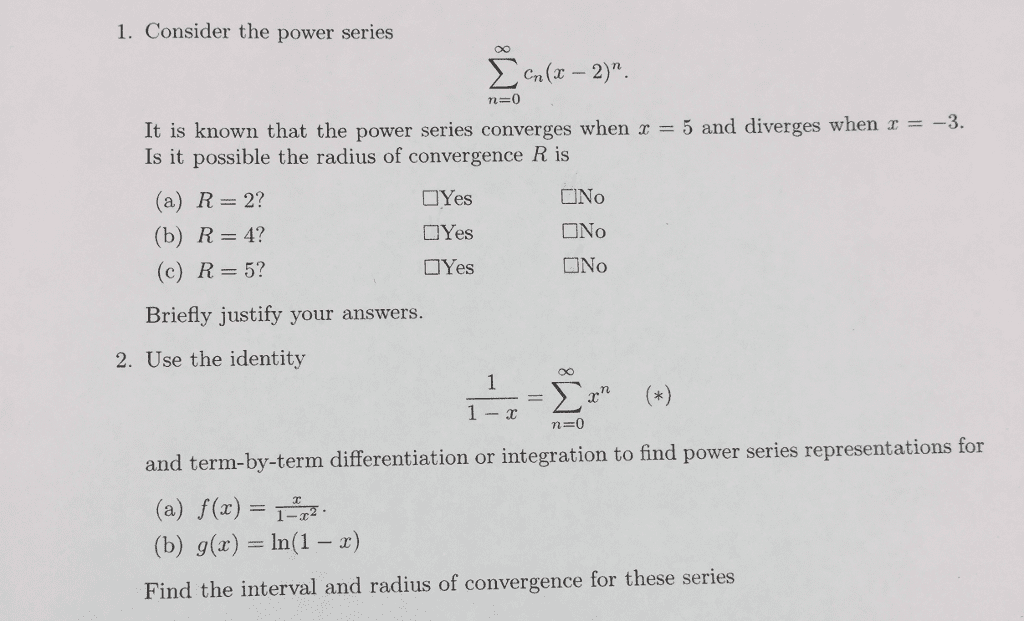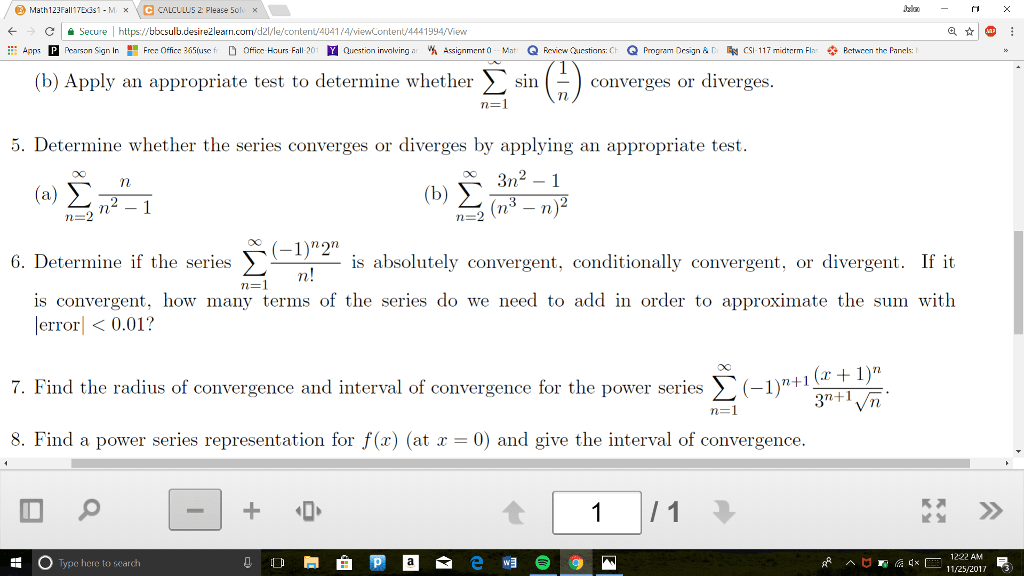MATH 3600 Midterm: MATH 3600 Iowa Spring15 Exam2odExam 2016ANS
Document Summary
Find the radius of convergence of the power series p n=2 an+1 an. Thus the series converges for all x such that |x 4| < 1. Note, you were not asked to nd all x for which the above power series converges, but we will do so anyway. We know the series diverges for all x such that |x 4| > 1. Thus we only need to check the endpoints of. 2 , 4 + 1 ( 2)n(x 4)n ( 2)n( 1. 2 )n ( 2)n( 7 n2 n=2 n=2 n2 n2. = p converges for all x [ 7 ( 1)n n=2 n2. Both these series converge and thus the series p . Thus if f (x) = p ( 2)n(x 4)n n=2 n2 ( 2)n( 1. , the largest possible domain for f is [ 7. Circle t for true and f for false.