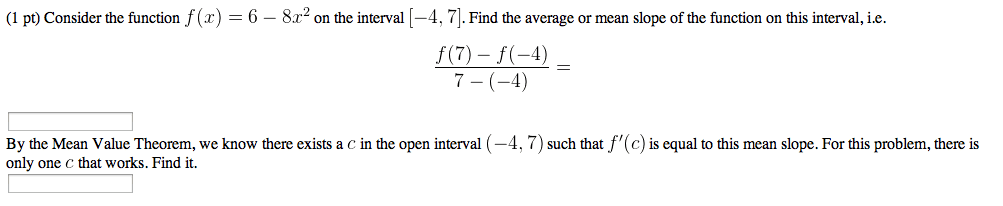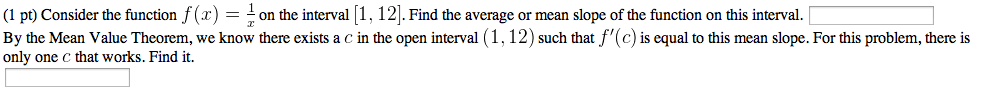MATH1151 Chapter Notes - Chapter 3: Uch, Indeterminate Form, Minimax
Document Summary
Suppose that f : (a, b) r. we say that f has a local maximum at a point c (a, b) if there is a small interval. I = (c , c + ) on which f (c) f (x), for all x i. We say that c is a local maximum point. A local extreme point is one which is either a local max or a local min. Then there exists at least one point c (a, b) such that f 0(c) = f (b) f (a) (b a) f (b) f (a) slope = f (b) f (a) = f 0(c) a c b: example. Let f : [1, 3], f (x) = x 3. Take a = 1 and b = 3, then the slope between the endpoints is f (b) f (a) (b a) Now f is differentiable on (1, 3) with f 0(x) = 3x 2.