MATH 302 Chapter Notes - Chapter 1.5: Linear Inequality, Free Variables And Bound Variables, Solution Set
Document Summary
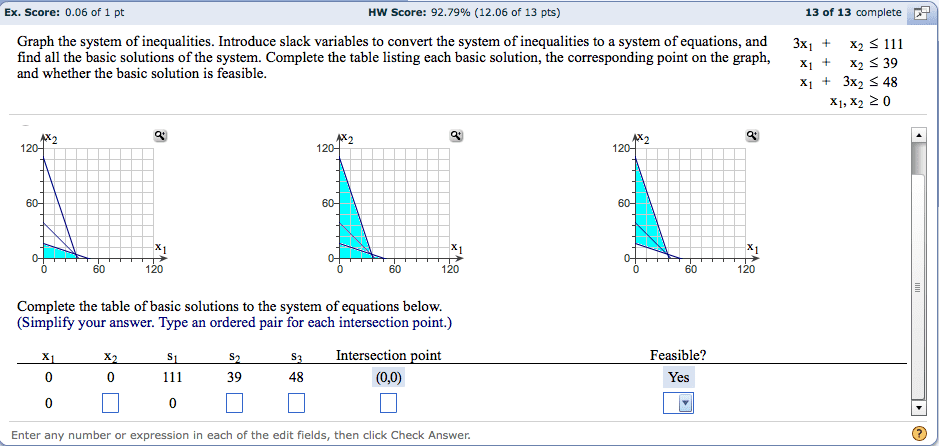
Linear inequality in two variables is simple ax+by , <= or >=, c. You may have a system of linear inequalities,that is you have multiple equations like these, and you need to find the solution set. To do this, you look at the answer to each linear inequality and then find the overlapping answers. Note: if these were not inequalities, but instead equations then if you had two variables, you may only have been able to solve two equations, or maybe 3 or more, by assuming one as a free variable. Anyways, you plot the graph for a linear inequality, this divides the area in two half planes. Then you look for a test point, on either of the half planes and see if it satisfies the inequality. That part of the plane is your answer to the inequality. You do that for all the linear equations, and the overlapping part is your answer.