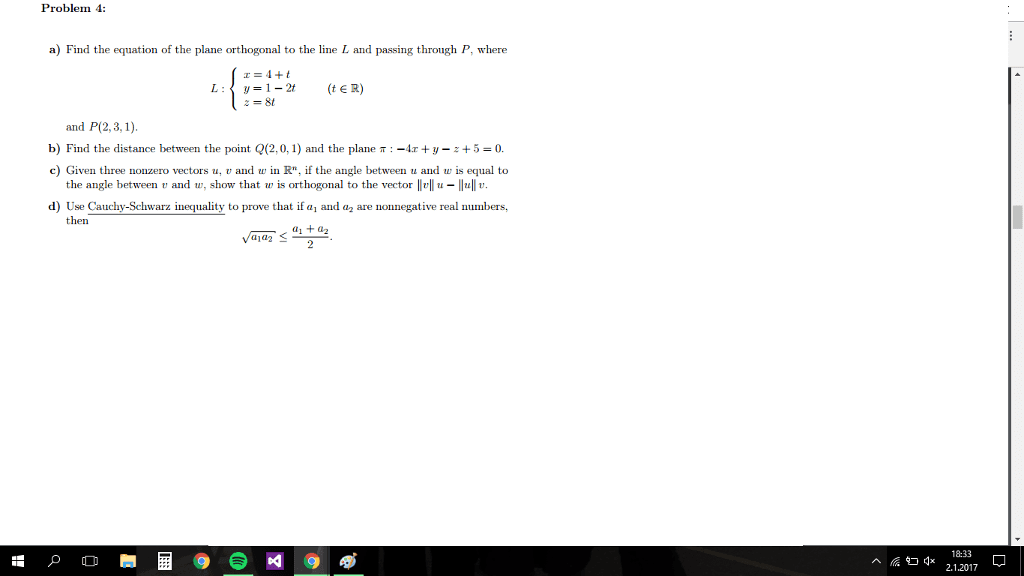MATH 1550 Chapter : Chap12sec5

12.5 Equations of Lines and Planes
A line L is determined by a point
0 0 0 0
,,P x y z
on L and the direction of L. The direction of a line is
described by a vector.
v
- vector parallel to L
( , , )P x y z
- an arbitrary point on L
0
,rr
- position vectors of P0 and P (representation vectors)
a
- vector with representation
0
PP
Triangle Law for vector addition gives
0
r r a
a
and
v
are parallel and there is a scalar
t
such that
a tv
.
0
r r tv
is the vector equation of L.
Each value of the parameter
t
gives the position vector
r
of a point on L.
0t
corresponds to points on L on one side of P0.
0t
corresponds to points on L on the other side of P0.
v
: vector that gives the direction of L
,,v a b c
is the direction of L in component form from which we can get
,,tv ta tb tc
.
0 0 0 0
, , , , ,r x y z r x y z
The vector equation of the line
0
r r tv
becomes
0 0 0
, , , ,x y z x ta y tb z tc
Two vectors are equal if and only if the corresponding components are equal.
The parametric equations of the line L through the point
0 0 0 0
,,P x y z
and parallel to the vector
,,v a b c
are:
0 0 0
x x at y y bt z z ct
x
y
z
L
v
P(x,y,z)
P0(x0,y0,z0)
r
r0
t=0
t>0
t<0
r0
a