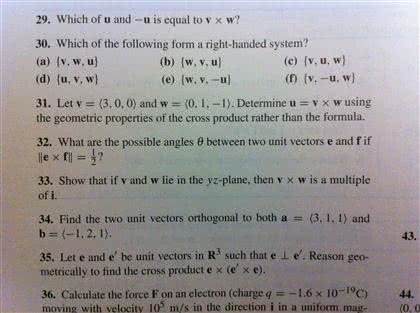MATH136 Lecture Notes - Triple Product, Right-Hand Rule, Anticommutativity

• School: University of Waterloo
• Department: Mathematics
• Course: MATH136
• Professor: Robert Andre

Document Summary

Wednesday, january 15 lecture 5 : cross-products in 3: cross product of two vectors in 3. In this lecture we introduce another operation on pairs of vectors in 3 called cross. 5. 1 definition given two vectors v = (a, b, c) and w = (x, y, z) in 3 the cross product: cross product properties u v is defined as follows: 5. 1. 1 example given a = (1, 3, 2) and b = (1, 1, 5) and c = (2, 2, 3) show that the cross product (b a) (c a) is (25, 7, 2). 5. 1. 2 example given two vectors v = (a, b, c) and w = (x, y, z) verify that the cross product u v belongs to the family of all vectors which are orthogonal to both v and. Let a, b and c be vectors in 3. Cp1 a b is a vector in 3.