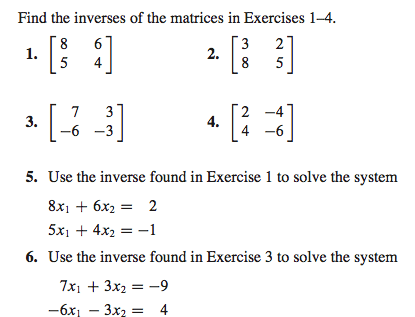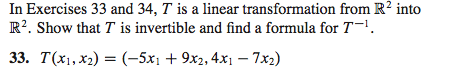MATH136 Lecture Notes - Gaussian Elimination, Augmented Matrix, Systemax

34
MATH136 Full Course Notes
Verified Note
34 documents
Document Summary
Monday, march 10 lecture 25 : invertible matrices. Concepts: define the inverse of a matrix, find the inverse of a matrix, solve a system by using the inverse of a matrix, recognize that a matrix is invertible if and only if its inverse has the rref. 25. 1 definition we say that an n n matrix a is invertible (or non-singular) if there exists an n n matrix b such that both conditions ab = in = ba hold true. We call such a matrix b, an inverse of a. Note that only a pair of square matrices of equal dimension can satisfy the condition ab. So if we refer to matrix a as being invertible then a must be a square matrix. 25. 1. 2 proposition uniqueness of the inverse of a matrix. Let a be an n n invertible matrix. Then there exists no more than one inverse b of a.