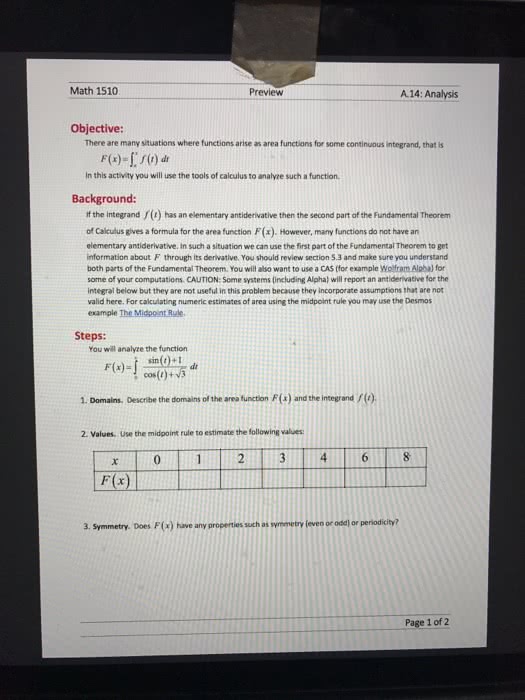
MAT 1320 Lecture Notes - Lecture 12: Riemann Sum, Antiderivative
31 Oct 2016
School
Department
Course
Professor
21
MAT 1320 Full Course Notes
Verified Note
21 documents
Document Summary
Lecture 12: integrals and the fundamental theorem of. 3) area under a curve: derivatives antiderivatives a. F(x) is an antiderivative of f(x) if definite integrals (riemann sum) Notice: derivatives and integrals are inverses of each other. Ex 2: what happens if we differentiate this? is continuous on [a,b] and differentiable on (a,b) and g"(x)=f(x) If f is continuous on [a,b], then: other notation: F is an antiderivative of f, but so is f(x)-f(a) because: is the same as f(x)-f(a) The fundamental theorem of calculus - part 2. If f is continuous on [a,b], then: such that f"(x)=f(x) connection between area under f(x) and its antiderivative! we can compute this as. So: where f(x) , an antiderivative of f(x). 5. 4 indefinite integrals (no bounds) ie. it does not matter which antiderivative we choose! Lectures page 2 then, for example: (f(x) is an antiderivative of f(x)) A few important integrals (see full table in textbook):
