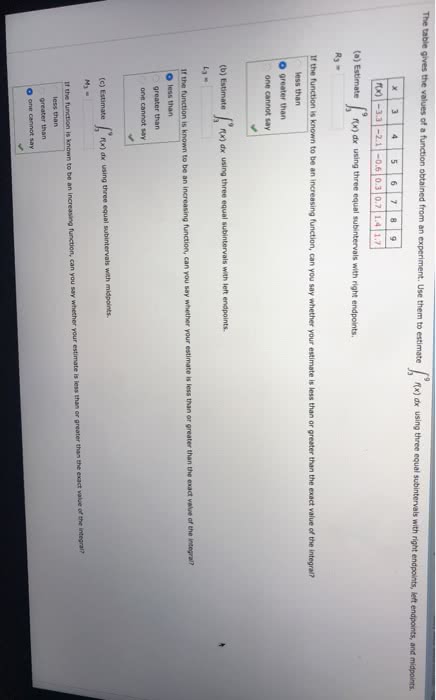
Find all solutions of the equation 3x - 7 = 4 = 0. Explain why you have found all the roots. Discuss this problem in class. Find all solutions of the quadratic equations x^2 + x --4 = 0. Explain why you have found all the roots. Discuss this problem in class. Apply the quadratic formula to the equation x^2 + x + 4. What difficulty do you encounter? Does this equation have any real roots? Draw the graph of p(x) = x^2 + x + 4 and discuss in class why there are no real roots. If a polynomial is to have real roots then its graph must cross the x-axis. Discuss in class why this is true. Then discuss why a cubic equation will always have at least one real root while a quadratic equation may not. Discuss in class whether a quartic (i.e., a fourth-degree) equation will always have a real root. Look at some examples. What about p(x) = x^4 + 1? What about x^4 - 2x^2 + 1? Use Cardano's method to find a root of the polynomial x^3 - x - 6. Use Cardano's method to find a root of the polynomial 3x^3 - 10x^2 + 9. Can you write down a polynomial whose roots are -1, 3, 5? Can you give an example of a polynomial of degree 2 that has no real roots? How about degree 4? Explain why a polynomial of odd degree at least 1 will always have at least one real root.
Show transcribed image text Find all solutions of the equation 3x - 7 = 4 = 0. Explain why you have found all the roots. Discuss this problem in class. Find all solutions of the quadratic equations x^2 + x --4 = 0. Explain why you have found all the roots. Discuss this problem in class. Apply the quadratic formula to the equation x^2 + x + 4. What difficulty do you encounter? Does this equation have any real roots? Draw the graph of p(x) = x^2 + x + 4 and discuss in class why there are no real roots. If a polynomial is to have real roots then its graph must cross the x-axis. Discuss in class why this is true. Then discuss why a cubic equation will always have at least one real root while a quadratic equation may not. Discuss in class whether a quartic (i.e., a fourth-degree) equation will always have a real root. Look at some examples. What about p(x) = x^4 + 1? What about x^4 - 2x^2 + 1? Use Cardano's method to find a root of the polynomial x^3 - x - 6. Use Cardano's method to find a root of the polynomial 3x^3 - 10x^2 + 9. Can you write down a polynomial whose roots are -1, 3, 5? Can you give an example of a polynomial of degree 2 that has no real roots? How about degree 4? Explain why a polynomial of odd degree at least 1 will always have at least one real root.