PHYS 2108 Lecture Notes - Lecture 8: Simple Harmonic Motion, Free Body Diagram, Stopwatch
8-1
LAB 8:
Simple Harmonic Motion
Hooke’s Law
We all have some familiarity with springs. If we stretch a spring away from its relaxed (unstretched)
length, if exerts a pulling force to try to return to its shorter state. Likewise, if we compress the spring, it
exerts a pushing force to try to return to its lengthened state. This is called a restoring force: a force
opposing the change to restore the system to its relaxed state.
For most springs, the relationship between restoring force and displacement from the relaxed state is
linear. For example, if we double the stretching (or compression), the force doubles. This relationship is
called Hooke’s Law, and any spring obeying it is called an ideal spring.
Eqn. 8-1
Hooke’s La
The negative sign is strictly a theoretical consideration to make the force vector in the opposite direction
of the displacement. In free body diagrams you only need to worry about the magnitude (because you
draw the vector in the correct direction). The coefficient k is called the spring constant and represents
the spig’s stiffess. A stiffe spring resists displacement more, so it has a higher k.
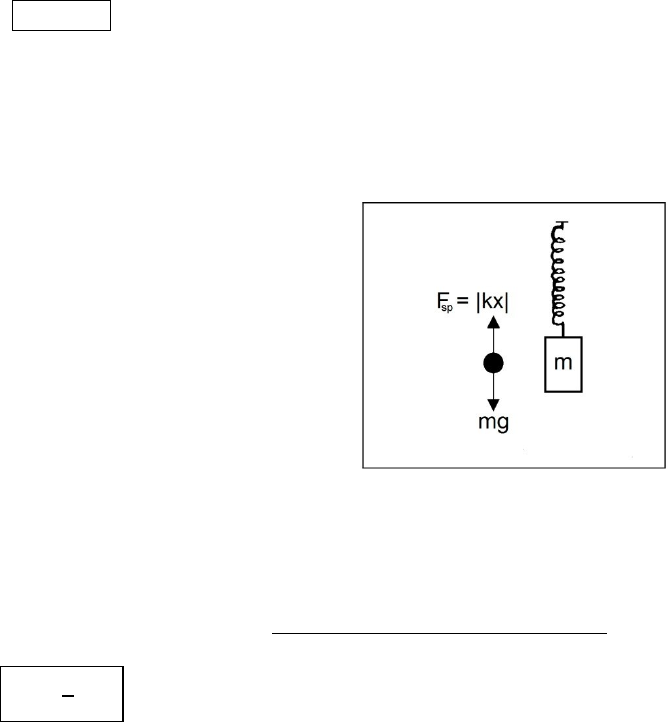
Consider the mass-spring system to the right. If it is in equilibrium,
the forces on it are balanced with equal magnitudes but opposite
directions. The downward force is of course just the weight of the
hanging mass. The spring counters this with its restoring force.
Hooke’s La depeds o us assuig the statig positio fo
displaeet easueets is at = 0. If it is ot, that’s oka. We
simply need to say the displacement is the difference in position
ad odif Hooke’s La as
.
Analyzing the free body diagram with a = 0,
Spring Potential Energy
Beause e’e applig a foe agaist the estoig foe through some displacement distance, e’e
doing work on the spring. That eas e’e stoig potetial eeg ito it.
Eqn. (8-2)
Spring Potential Energy
Real Springs
An ideal spig oes Hooke’s La lieal. A real spring is not as perfect. Most springs can be called
ideal eause the oe Hooke’s La fo sall displaeets. At soe poit the appoiatio eaks
do if it stethes too uh. I these egios the spig a peaetl defo o the etal ay
eake. Othe sstes oeig Hooke’s La pedula, ostl ae liea fo sall agles, ut eoe
e diffeet if the’e displaed too fa.
find more resources at oneclass.com
find more resources at oneclass.com

8-2
Simple Harmonic Motion
A ojet that oes Hooke’s La ill udego osillatio if distued fo its euiliiu positio. As
long as the restoring force is linear, the resulting oscillation is called simple harmonic motion.
The object must be excited to oscillate by giving it some energy. It can either be given kinetic energy at
its equilibrium position by striking it, or it can be given potential energy by being displaced away from its
equilibrium position. During the oscillation, the system is constantly trading its energy between KE and
PE forms.
Some key features are present in simple harmonic oscillation. The maximum displacement away from
equilibrium (and max PE, zero KE state) is called the amplitude (A) of oscillation. The amount of time for
the oscillator to make one complete cycle is called the period (T). The frequency (f) is how often the
osillato opletes les kid of like a speed i osillatios pe seond, or Hertz [Hz]).
The motion of a simple harmonic oscillator is described by
Tig futios ol ok o agles, so the agle must be considered to be in radians, not
degees. This is due to adias eig a atual uit oposed of atios.
If a osillato’s feue is 3 osillatios/s o 3 Hz, for example, then each oscillation takes 1/3 of a
seod to oplete. B eaple e’e shoed the peiod of osillatio ad frequency are reciprocal of
one another.
Eqn. 8-3
Period and Frequency
The frequency of oscillations depends on how easily the spring can move the attached mass. The
resulting period depends upon the systems parameters k and m as:
Eqn. 8-4
Period for Ideal Spring-Mass
find more resources at oneclass.com
find more resources at oneclass.com
Document Summary
If we stretch a spring away from its relaxed (unstretched) length, if exerts a pulling force to try to return to its shorter state. Likewise, if we compress the spring, it exerts a pushing force to try to return to its lengthened state. This is called a restoring force: a force opposing the change to restore the system to its relaxed state. For most springs, the relationship between restoring force and displacement from the relaxed state is linear. For example, if we double the stretching (or compression), the force doubles. This relationship is called hooke"s law, and any spring obeying it is called an ideal spring. The negative sign is strictly a theoretical consideration to make the force vector in the opposite direction of the displacement. In free body diagrams you only need to worry about the magnitude (because you draw the vector in the correct direction). The coefficient k is called the spring constant and represents the sp(cid:396)i(cid:374)g"s stiff(cid:374)ess.

