MATH 1151 Lecture Notes - Lecture 26: Minimax

• School: Ohio State University
• Department: Mathematics
• Course: MATH 1151
• Professor: Ernest Fontes

Document Summary

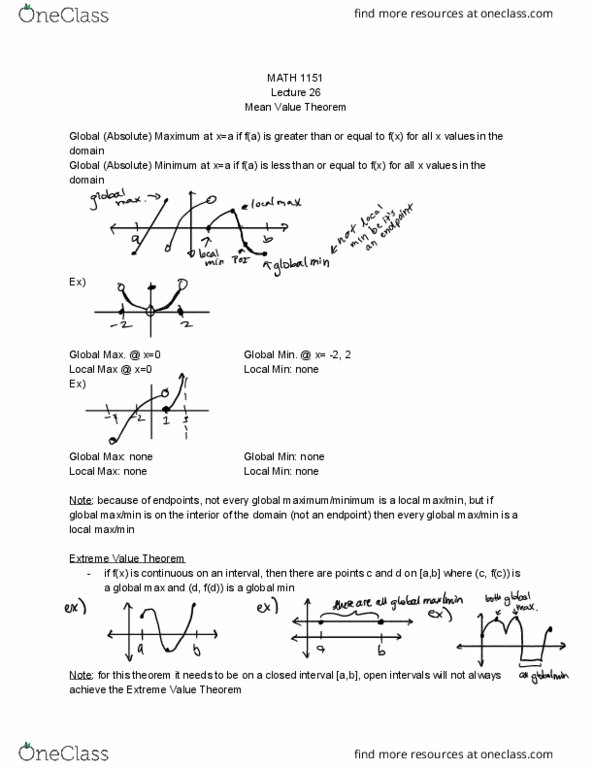
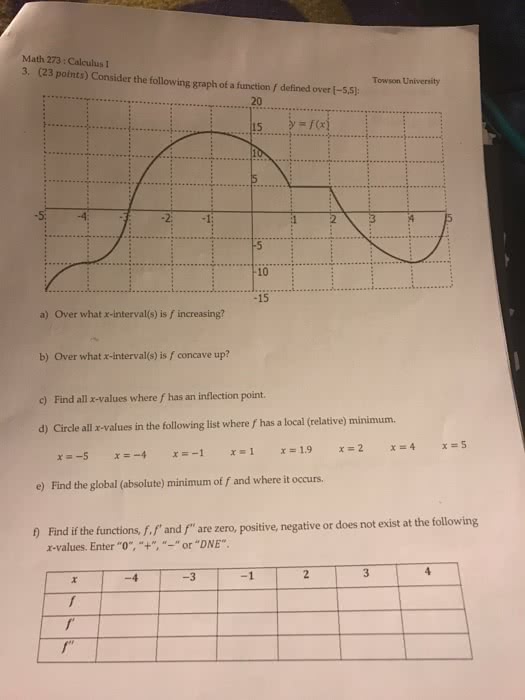
O ca o alocal 94 min poi qglobalmin. Global (absolute) maximum at x=a if f(a) is greater than or equal to f(x) for all x values in the domain. Global (absolute) minimum at x=a if f(a) is less than or equal to f(x) for all x values in the domain. Note : because of endpoints, not every global maximum/minimum is a local max/min, but if global max/min is on the interior of the domain (not an endpoint) then every global max/min is a local max/min. Local min: none t. it if f(x) is continuous on an interval, then there are points c and d on [a,b] where (c, f(c)) is a global max and (d, f(d)) is a global min my. Note : for this theorem it needs to be on a closed interval [a,b], open intervals will not always achieve the extreme value theorem il am aceglobalnun.