Answer the questions based on the article provided
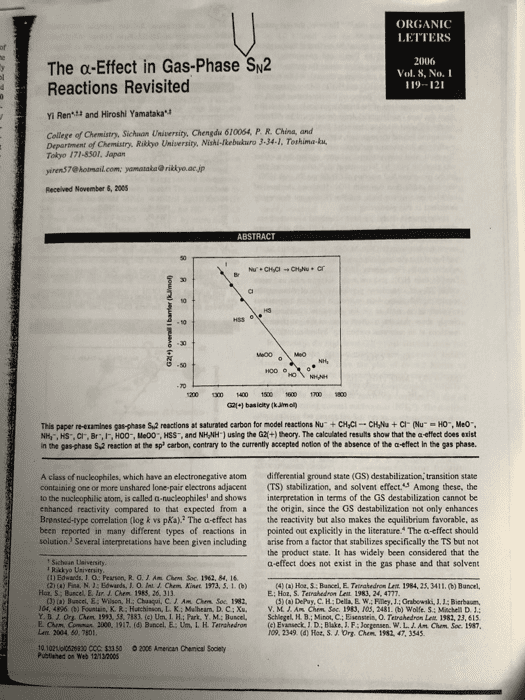
ORGANIC LETTERS The α-Effect in Gas-Phase%2 Reactions Revisited 2006 Vol. 8, No.I 119-121 : Yi Ren and Hiroshi Yamatakau College of Chemistry, Sichuon University, Chengdu 610064, P. R. China, and Department of Chemistry. Riklyo University, Nishi-kebukuro 3-34-1, Tothima-ku Tokyo 171-8301, Japan yiren$7@ hotmail.com [email protected] jp Received November 6, 2005 50 G21+1 basicity (kJimo This papenetamines gasphase sa reactions at saturated carbon for model reactionshu, cyc-cvu + cr our 'O., Meo-. NH,, HS-. CI, Br,IF, HO0-, Me00", HSS, and NHNH1 using the G2+) theory. The calculated results show that the a effect does exist in the gas-phase S,2 reaction at the sp carbon, contrary to the currently sccepted notion of the absence of the a-effect In the gas phase A class of nucleophiles, which have an electronegative atom differential ground state (GS) destabilization, transition state containing one or more unshared lone pair electrons adjacent (TS) stabilization, and solvent effect.S Among these, the o the nucleophilic atom, is called a-nucleophiles and shows interpretation in terms of the GS destabilization cannot be enhanced reactivity compared to that expected from a the origin, since the GS destabilization not only enhances the reactivity but also makes the equilibrium favorable, as pointed out explicitly in the literature. The a-effect should solution. Several inserpretations have been given including arise from a factor that stabilizes specifically the TS but no the product state. It has widely been considered that the a-effect does not exist in the gas phase and that solvent Brensted-type correlation (log k vs pKa).2 The a-effect has been reported in many different types of reactions in Sichaan Uaiversity Rakkyo Usiversity (1) Edwards. J. O: Pearson, R.G.JAm Chem Soc. 1962, 84, 16 4) () Hot, S Bancel, E. Tatrahedron Let 1984, 25, 3411. (b) Buncel Hot, S; Buncel, E. lur. J. Chem 1983, 26, 313 E: Hor, S. Terrahedron Leit 1983, 24, 4777 CJ) (a) Buscel,E:Wilson, H: Chaaqui, C. Am Ohm Soc. 1982 (5) (a) DePuy, C. H; Della, E W; Filey, J.: Grabewski, J1.1: Bierbaum, V.M.J.Aå¤CMm Soc. 1983. 10.5. 2481,(b) wolfes:sehela D 1: 04, 4896 (b) Fountain, K. RiHatchinson, L. K: Mulhearn. D. C ; Xu, Y. B J. Ora aen. 199. 58. 7183, (c) UnãLFL; Park. Y M.; Bunced. Lenx. 2004 50, 7801 10 1021lpl0528830 CCC: $33 50 2006 American Chenical Soclety Schlegel, H B.; Minot, C.; Eisenstein, 0. Telahedran Lat 1982, 23, 61s (c) Evatieck, J D: Blake, J. F; Jorgensen. w.L. ro9. 2349 (d) Hot. S.J. Org. arm. Conu, 2000, 1917. (d) Bancel, E.-Un. I, H. Ternshedro, Am Cham. Soc. t987 1982, 47, 3545 Publined on web 12-1200S
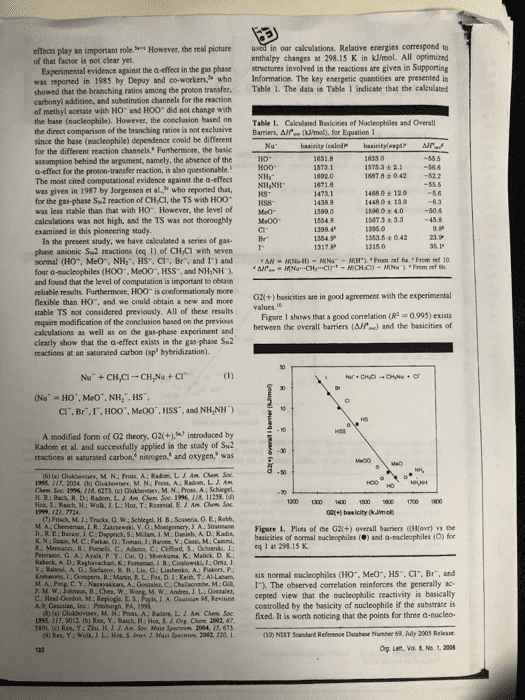
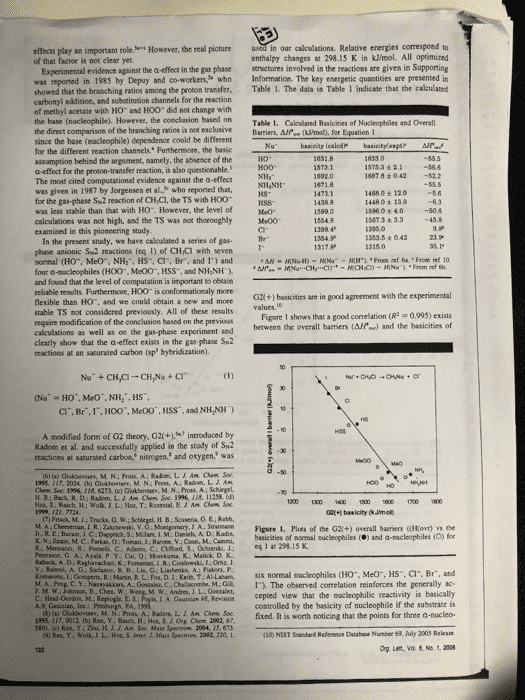
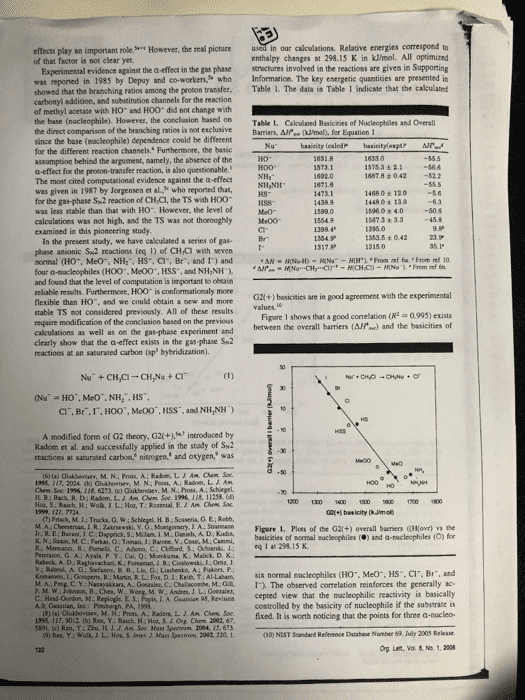
effects play an important role of that factor is not clear yet. However, the real picture in our calculations. Relative energies correspond to enthalpy changes at 298.15 K in kJ/mol. All optimized Experimental evidence against the a-effect in the gas phase structures involved in the reactions are given in Supporting was reported in 1985 by Depuy and co-workers who Information. The key energetic quantities are presented in showed that the branching ratios among the proton transfer. Table 1. The data in Table 1 indicate that the calculated carbonyl addition, and substination channels for the reaction of methyl acetate with HO and HOO did not change with the base (nucleophile). However, the conclasion based on Table 1. Cakculated Basicities of Nucleophiles and Overall the direct comparison of the branching ratios is not exclusiveBarriers, Afe (ml, for Equation 1 since the base (nocleophile) dependence conld be different for the different reaction channels. Furthermore, the basic assamption behind the argument, aamely, the absence of the a-effect for the proton-transfer reaction, is also questionable. The most cited computational evidence against the a-effect was given in 1987 by Jorgensen et al, who reported that, for the gas-phase Sw2 reaction of CH Cl, the TS with HOO was less stable than that with H0. However, the level of calculations was not high, and the TS was not thoroughly Me00 examined in this pioncering study İSTsa ± 2.1-56.6 1487.8 +042 52.2 14680± 120 1448 0 t 13o 15960 + 4.050.4 15673 + 3.3 45.8 kS- 1353.5 ± O 42 In the present study, we have cakculated a series of gas phase anionic Sw2 reactions (eq 1) of CHCi with seven normal (HO, MeO, NH:, HS, Cl, Br, and 1) and four a-sacleophiles (H00, Me00, HSS, and NH,NH and found that the level of computation is important to obeain reliable results. Furthermoee, HOO is conformationaly more flexible than HO. and we could obtain a new and mone stable TS not considered previously. All of these results require modification of the conclusion based on the previous calculations as well as on the gas-phase experiment and clearly show that the a-effect exists in the gas phase Su2 reactions at an saturated carbon (sp hybridization). G2l(+) basicities are in good agreement with the experimental Figare 1 shows that a good correlation (R 0993) exists between the overall barriers (AH) and the basicities of CI. Br.I,HOO", McOO, HSS, and NH,NH) A modified form of G2 theory, G2(+.introduced by Radom et al. and successfully applied in the stady of Sk2 reactices at saturated carbon, nitrogen, and oxygen, was (t) (a) Glakbevsev, M. N.; Pros, A: Radom, LIAM hem Soe 195. 117. 2024 (b) Ghshovtev, M. N: Post, A; Radom. L. J Am H B; Bach, R. D: Radom, L. A. Am Chem Soe 1996, 118, 11258.( 1200 1300 1 150 600700 1800 (7) Frisch, M.14 Trucka, O.W M A Cheeseman JR. Zkrski, V. G: Monigomery, J A: Suatmann Figere 1. Plots of the G2(+) overall barriers ((Ho) the basicities of mormal nucleophiles () and a-nucleophiles (O) for K. N.: Szain, M.C Farkas, O: Tomasi, J:Barone, V.: Cossi, M: Cammi, Priersion, G A.: Ayala P. Y. Cui, Q:Mokuma, K Malick. D. K. v.: Baboul. A. Stefanov. B 11,Lis. G ; Liashenko, A; Paker, P. eq 1 at 298 15 K Kom-ne t Go pens R Main R L. Fo. Ket), T AI Laham, six normal nucleophiles CHO.. Meo", HS, Cr. Br, and D C Y. Nanayakkars, A. Gonaaler, C.Chalacombe, M.1. The observed correlation reinforces the generally ac- L. A. Gearsian 95, Revisicn cepted view that the macleophilic reactivity is basically controlled by the basicity of nucleophile if the substrate is 02fixed. It is worth noticing that the points for three a-nucleo- (10) NIST Sandard Refenence Database Number 69, July 2003 Rekase Org Lent, Vol & No. 1, 2006 A., Guastian, Inc Bc HH Ch 5191. (c) Ren, Y: Zhu, H. J. J. Am Soc Mass Spectron 2004, 15, 673 9) Res, Y: Wolk JL. Hoa, S. Jnter, J. Mass Spectron 2082, 220, 1
philes out of the four examined deviate downward from the (by 8.7 k/mol) than the trans one probably due to the correlation line, displaying detectable a-effect in the S2 favorable electrostatic interaction betaween the a-atom (0) raction. The point for NH&NH- is slightly above the line, in HO0 and the positively charged methyl moiety at the but this nocleophile is more reactive than NH3" despite its TS. Such interaction is weaker in the trans conformer smaller basicity, as can be seen in Figure 1:It should also NH Ys NH,NH-. In these two cases the attacking atoms be noted that both MeO" and HO" behave normally, whereas are nitrogen. The calculated gas-phase basicity of NH NH HOO-deviates downward from the correlation line. The is smaller than N, by 20.4 klimol, whereas the results indicate that the deviation of HOO-is not due to the size effect, namely, an extra stability due to a polarizabiliry effect, often observed in the gas-phase calculations for a large species. The four pairs of the normal and corresponding be higher for NH NH than for NH a-nucleophiles are compared in detail below for the reaction of NH,NH' + CH,Cis lower than that for NH +CH/CI by 3.3 kJ/mol. This leads to the expectation that the reaction efficiency for the gas-phase reaction should HS vs HSS. The attacking atoms are sulfur in these HO- vs HO0. The reaction of HO +CH,CI has been two nucleophiles. The calculated G2(+) AH values in extensively studied experimentally" and computatonallyn Table l show that he ÎÎ s 6.3 kJ mol for the reaction The reaction of HOO +CHCI is less studied theoretically of a-nucleophile HSS with CH,CI, slightly lower than that and only calculated at a lower level. The caleulations by for HS with CH,CI by 0.7 kJ/mol, even though HSS is Jorgensen et al. at the MPn 2 and 3WHF6-31+G less basic than HS- by 34.3 kJ/mol. Thus, the a-effect is level of theory suggested that the Alf'o. for HO+CHCI clearly observed. is lower than that for HOO CH,CI by more than 10 MeO vs Me00. The calculated overal kl/mol. However, the present study revealed that the TSs for reactions of HO+CH,Cl and HO0+CHCl are 55.5 and 56.6 kJ/mol below the reactants at the G20+) level, barrier for Meo-t, СÐÐ is-506 klrnel, which is higher than that for HO+CH CI by 4.9 kJ/mol, consistent with the smaller basicity of MeO" in the gas phase. Although the Alf for respectively, thas indicating that H00- is more reactive than a-nucleophile MeOO" is slightly higher than that for Meo HO, even though HOO. is a much weaker base than HO.. by 48 k1ml due to its smaller basicity and stenc effects. The different results can be attributed to the different TS there is still a obvious downward deviation for Me00 in es for the reaction of HOO; we found a new TS Figure 1. This result again confirms the a-effect in the gas- with a skew conformer (Figure 2, C-O-0-H 108.5°), phase Sw2 reaction. The TS prefers the skew conformation (C-0-0-C 103.8°) due to the favorable interaction between the a-atom with the methyl moiety as in the case In sammary, the high level G2(+) calculations show that three out of the four a-nucleophiles examined exhibit downward deviation from the plot of overall barrier vs basicity and accelerate the reaction through the stabilizatiorn of the transition stractures.The other a-nucleophile (NH,NH) clearly shows an enhanced reactivity compared to that of the corresponding normal nacleophile (NH2"). The a-effect does exist in the gas-phase Sx2 reaction at saturated carbon, contrary to the currently accepled notion of the absence of the a -effect in the gas phase. skew-conformer (0.0 kWmol Acknowledgment. Y.R. thanks Japan Society for the Promotion of Science for the invication Fellowship Programs for Research in Japan (no. L05546). H.Y. thanks Rikkyo Umiversity Fromtier Project "Life's Adaptation Strategies to Environmental Changes Figure 2. Two different TSs in the reaction of HOO" +CH.CI All atomic distances are in angstroms and angles are in degrees. The values in parentheses are relative enthalpies at 298.15 Supporting Information Available: Optimized geom- etries and G2(+) enthalpies at 298.15 K of all species in eq I. This material is available free of charge via the Intermet at http:llpubs.acs.org. addition to the trans conformer (C-0-0-H 180.0) ed previously N The skew conformation is more stable OL0S26930 (12) (a) Evanseck, J. D; Blake, 1. F:Jorgense, W.L. A An Chen Soe. 1987, 109, 2349 (b) Re. S:Morokuma, K. J. Phyt. Chem. A 2001, 1) (a) Henchman, M; Paulson, J. F Hiert P.M. J Am Chen. Soe 2002, 106, 10977 A. A: Paciso, J. F.: Clary, D. C.J Am. Chem. Soc. 1986, 408, 3142 Lat, Vol 8,â1" 2006
Read the paper titled "The a-effect in gas-phase SN2 reaction revisited" (Ren, Y, Yamataka, H. Org. Lett., 2006, 8, 119-121) You will answer the following questions. 1. What is the a-effect? 2. In the first paragraph, they talk about the comparison between reactivity and acid-base: log k vs pKa. Why is that? 3. What is the central thesis of the paper?
Show transcribed image text ORGANIC LETTERS The α-Effect in Gas-Phase%2 Reactions Revisited 2006 Vol. 8, No.I 119-121 : Yi Ren and Hiroshi Yamatakau College of Chemistry, Sichuon University, Chengdu 610064, P. R. China, and Department of Chemistry. Riklyo University, Nishi-kebukuro 3-34-1, Tothima-ku Tokyo 171-8301, Japan yiren$7@ hotmail.com [email protected] jp Received November 6, 2005 50 G21+1 basicity (kJimo This papenetamines gasphase sa reactions at saturated carbon for model reactionshu, cyc-cvu + cr our 'O., Meo-. NH,, HS-. CI, Br,IF, HO0-, Me00", HSS, and NHNH1 using the G2+) theory. The calculated results show that the a effect does exist in the gas-phase S,2 reaction at the sp carbon, contrary to the currently sccepted notion of the absence of the a-effect In the gas phase A class of nucleophiles, which have an electronegative atom differential ground state (GS) destabilization, transition state containing one or more unshared lone pair electrons adjacent (TS) stabilization, and solvent effect.S Among these, the o the nucleophilic atom, is called a-nucleophiles and shows interpretation in terms of the GS destabilization cannot be enhanced reactivity compared to that expected from a the origin, since the GS destabilization not only enhances the reactivity but also makes the equilibrium favorable, as pointed out explicitly in the literature. The a-effect should solution. Several inserpretations have been given including arise from a factor that stabilizes specifically the TS but no the product state. It has widely been considered that the a-effect does not exist in the gas phase and that solvent Brensted-type correlation (log k vs pKa).2 The a-effect has been reported in many different types of reactions in Sichaan Uaiversity Rakkyo Usiversity (1) Edwards. J. O: Pearson, R.G.JAm Chem Soc. 1962, 84, 16 4) () Hot, S Bancel, E. Tatrahedron Let 1984, 25, 3411. (b) Buncel Hot, S; Buncel, E. lur. J. Chem 1983, 26, 313 E: Hor, S. Terrahedron Leit 1983, 24, 4777 CJ) (a) Buscel,E:Wilson, H: Chaaqui, C. Am Ohm Soc. 1982 (5) (a) DePuy, C. H; Della, E W; Filey, J.: Grabewski, J1.1: Bierbaum, V.M.J.Aå¤CMm Soc. 1983. 10.5. 2481,(b) wolfes:sehela D 1: 04, 4896 (b) Fountain, K. RiHatchinson, L. K: Mulhearn. D. C ; Xu, Y. B J. Ora aen. 199. 58. 7183, (c) UnãLFL; Park. Y M.; Bunced. Lenx. 2004 50, 7801 10 1021lpl0528830 CCC: $33 50 2006 American Chenical Soclety Schlegel, H B.; Minot, C.; Eisenstein, 0. Telahedran Lat 1982, 23, 61s (c) Evatieck, J D: Blake, J. F; Jorgensen. w.L. ro9. 2349 (d) Hot. S.J. Org. arm. Conu, 2000, 1917. (d) Bancel, E.-Un. I, H. Ternshedro, Am Cham. Soc. t987 1982, 47, 3545 Publined on web 12-1200S
effects play an important role of that factor is not clear yet. However, the real picture in our calculations. Relative energies correspond to enthalpy changes at 298.15 K in kJ/mol. All optimized Experimental evidence against the a-effect in the gas phase structures involved in the reactions are given in Supporting was reported in 1985 by Depuy and co-workers who Information. The key energetic quantities are presented in showed that the branching ratios among the proton transfer. Table 1. The data in Table 1 indicate that the calculated carbonyl addition, and substination channels for the reaction of methyl acetate with HO and HOO did not change with the base (nucleophile). However, the conclasion based on Table 1. Cakculated Basicities of Nucleophiles and Overall the direct comparison of the branching ratios is not exclusiveBarriers, Afe (ml, for Equation 1 since the base (nocleophile) dependence conld be different for the different reaction channels. Furthermore, the basic assamption behind the argument, aamely, the absence of the a-effect for the proton-transfer reaction, is also questionable. The most cited computational evidence against the a-effect was given in 1987 by Jorgensen et al, who reported that, for the gas-phase Sw2 reaction of CH Cl, the TS with HOO was less stable than that with H0. However, the level of calculations was not high, and the TS was not thoroughly Me00 examined in this pioncering study İSTsa ± 2.1-56.6 1487.8 +042 52.2 14680± 120 1448 0 t 13o 15960 + 4.050.4 15673 + 3.3 45.8 kS- 1353.5 ± O 42 In the present study, we have cakculated a series of gas phase anionic Sw2 reactions (eq 1) of CHCi with seven normal (HO, MeO, NH:, HS, Cl, Br, and 1) and four a-sacleophiles (H00, Me00, HSS, and NH,NH and found that the level of computation is important to obeain reliable results. Furthermoee, HOO is conformationaly more flexible than HO. and we could obtain a new and mone stable TS not considered previously. All of these results require modification of the conclusion based on the previous calculations as well as on the gas-phase experiment and clearly show that the a-effect exists in the gas phase Su2 reactions at an saturated carbon (sp hybridization). G2l(+) basicities are in good agreement with the experimental Figare 1 shows that a good correlation (R 0993) exists between the overall barriers (AH) and the basicities of CI. Br.I,HOO", McOO, HSS, and NH,NH) A modified form of G2 theory, G2(+.introduced by Radom et al. and successfully applied in the stady of Sk2 reactices at saturated carbon, nitrogen, and oxygen, was (t) (a) Glakbevsev, M. N.; Pros, A: Radom, LIAM hem Soe 195. 117. 2024 (b) Ghshovtev, M. N: Post, A; Radom. L. J Am H B; Bach, R. D: Radom, L. A. Am Chem Soe 1996, 118, 11258.( 1200 1300 1 150 600700 1800 (7) Frisch, M.14 Trucka, O.W M A Cheeseman JR. Zkrski, V. G: Monigomery, J A: Suatmann Figere 1. Plots of the G2(+) overall barriers ((Ho) the basicities of mormal nucleophiles () and a-nucleophiles (O) for K. N.: Szain, M.C Farkas, O: Tomasi, J:Barone, V.: Cossi, M: Cammi, Priersion, G A.: Ayala P. Y. Cui, Q:Mokuma, K Malick. D. K. v.: Baboul. A. Stefanov. B 11,Lis. G ; Liashenko, A; Paker, P. eq 1 at 298 15 K Kom-ne t Go pens R Main R L. Fo. Ket), T AI Laham, six normal nucleophiles CHO.. Meo", HS, Cr. Br, and D C Y. Nanayakkars, A. Gonaaler, C.Chalacombe, M.1. The observed correlation reinforces the generally ac- L. A. Gearsian 95, Revisicn cepted view that the macleophilic reactivity is basically controlled by the basicity of nucleophile if the substrate is 02fixed. It is worth noticing that the points for three a-nucleo- (10) NIST Sandard Refenence Database Number 69, July 2003 Rekase Org Lent, Vol & No. 1, 2006 A., Guastian, Inc Bc HH Ch 5191. (c) Ren, Y: Zhu, H. J. J. Am Soc Mass Spectron 2004, 15, 673 9) Res, Y: Wolk JL. Hoa, S. Jnter, J. Mass Spectron 2082, 220, 1
philes out of the four examined deviate downward from the (by 8.7 k/mol) than the trans one probably due to the correlation line, displaying detectable a-effect in the S2 favorable electrostatic interaction betaween the a-atom (0) raction. The point for NH&NH- is slightly above the line, in HO0 and the positively charged methyl moiety at the but this nocleophile is more reactive than NH3" despite its TS. Such interaction is weaker in the trans conformer smaller basicity, as can be seen in Figure 1:It should also NH Ys NH,NH-. In these two cases the attacking atoms be noted that both MeO" and HO" behave normally, whereas are nitrogen. The calculated gas-phase basicity of NH NH HOO-deviates downward from the correlation line. The is smaller than N, by 20.4 klimol, whereas the results indicate that the deviation of HOO-is not due to the size effect, namely, an extra stability due to a polarizabiliry effect, often observed in the gas-phase calculations for a large species. The four pairs of the normal and corresponding be higher for NH NH than for NH a-nucleophiles are compared in detail below for the reaction of NH,NH' + CH,Cis lower than that for NH +CH/CI by 3.3 kJ/mol. This leads to the expectation that the reaction efficiency for the gas-phase reaction should HS vs HSS. The attacking atoms are sulfur in these HO- vs HO0. The reaction of HO +CH,CI has been two nucleophiles. The calculated G2(+) AH values in extensively studied experimentally" and computatonallyn Table l show that he ÎÎ s 6.3 kJ mol for the reaction The reaction of HOO +CHCI is less studied theoretically of a-nucleophile HSS with CH,CI, slightly lower than that and only calculated at a lower level. The caleulations by for HS with CH,CI by 0.7 kJ/mol, even though HSS is Jorgensen et al. at the MPn 2 and 3WHF6-31+G less basic than HS- by 34.3 kJ/mol. Thus, the a-effect is level of theory suggested that the Alf'o. for HO+CHCI clearly observed. is lower than that for HOO CH,CI by more than 10 MeO vs Me00. The calculated overal kl/mol. However, the present study revealed that the TSs for reactions of HO+CH,Cl and HO0+CHCl are 55.5 and 56.6 kJ/mol below the reactants at the G20+) level, barrier for Meo-t, СÐÐ is-506 klrnel, which is higher than that for HO+CH CI by 4.9 kJ/mol, consistent with the smaller basicity of MeO" in the gas phase. Although the Alf for respectively, thas indicating that H00- is more reactive than a-nucleophile MeOO" is slightly higher than that for Meo HO, even though HOO. is a much weaker base than HO.. by 48 k1ml due to its smaller basicity and stenc effects. The different results can be attributed to the different TS there is still a obvious downward deviation for Me00 in es for the reaction of HOO; we found a new TS Figure 1. This result again confirms the a-effect in the gas- with a skew conformer (Figure 2, C-O-0-H 108.5°), phase Sw2 reaction. The TS prefers the skew conformation (C-0-0-C 103.8°) due to the favorable interaction between the a-atom with the methyl moiety as in the case In sammary, the high level G2(+) calculations show that three out of the four a-nucleophiles examined exhibit downward deviation from the plot of overall barrier vs basicity and accelerate the reaction through the stabilizatiorn of the transition stractures.The other a-nucleophile (NH,NH) clearly shows an enhanced reactivity compared to that of the corresponding normal nacleophile (NH2"). The a-effect does exist in the gas-phase Sx2 reaction at saturated carbon, contrary to the currently accepled notion of the absence of the a -effect in the gas phase. skew-conformer (0.0 kWmol Acknowledgment. Y.R. thanks Japan Society for the Promotion of Science for the invication Fellowship Programs for Research in Japan (no. L05546). H.Y. thanks Rikkyo Umiversity Fromtier Project "Life's Adaptation Strategies to Environmental Changes Figure 2. Two different TSs in the reaction of HOO" +CH.CI All atomic distances are in angstroms and angles are in degrees. The values in parentheses are relative enthalpies at 298.15 Supporting Information Available: Optimized geom- etries and G2(+) enthalpies at 298.15 K of all species in eq I. This material is available free of charge via the Intermet at http:llpubs.acs.org. addition to the trans conformer (C-0-0-H 180.0) ed previously N The skew conformation is more stable OL0S26930 (12) (a) Evanseck, J. D; Blake, 1. F:Jorgense, W.L. A An Chen Soe. 1987, 109, 2349 (b) Re. S:Morokuma, K. J. Phyt. Chem. A 2001, 1) (a) Henchman, M; Paulson, J. F Hiert P.M. J Am Chen. Soe 2002, 106, 10977 A. A: Paciso, J. F.: Clary, D. C.J Am. Chem. Soc. 1986, 408, 3142 Lat, Vol 8,â1" 2006
Read the paper titled "The a-effect in gas-phase SN2 reaction revisited" (Ren, Y, Yamataka, H. Org. Lett., 2006, 8, 119-121) You will answer the following questions. 1. What is the a-effect? 2. In the first paragraph, they talk about the comparison between reactivity and acid-base: log k vs pKa. Why is that? 3. What is the central thesis of the paper?