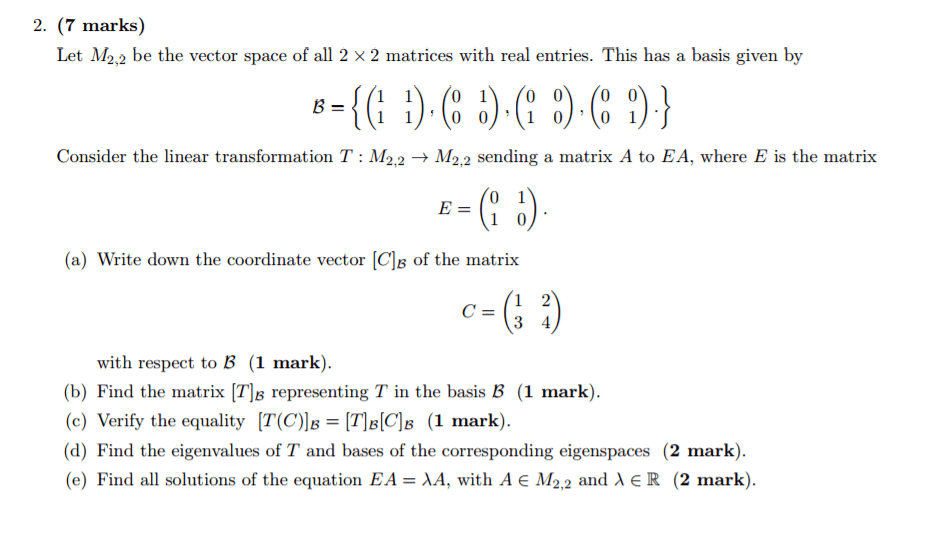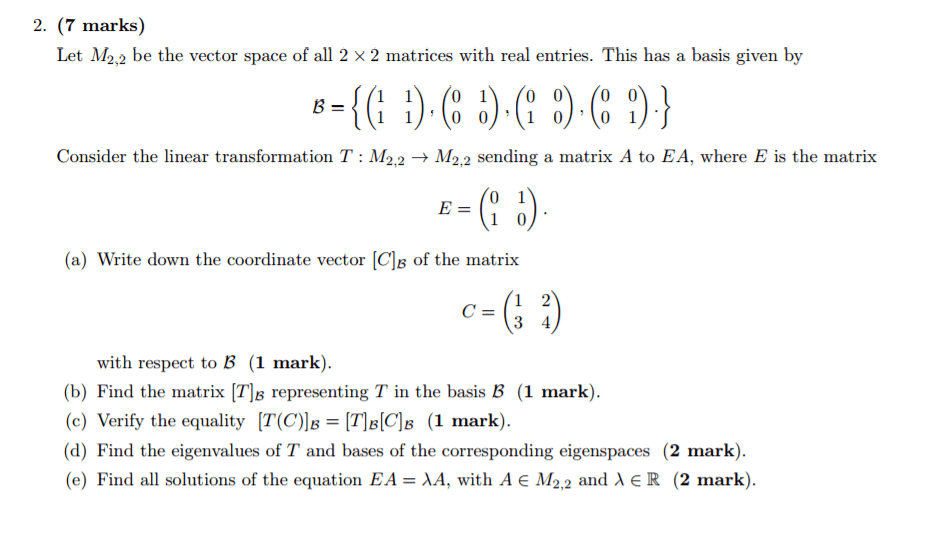
Let M_2, 2 be the vector space of all 2 times 2 matrices with real entries. This has a basis given by B = {(1 1 1 1), (0 0 1 0), (0 1 0 0), (0 0 1 0), (0 0 0 1)} Consider the linear transformation T: M_2, 2 rightarrow M_2, 2 sending a matrix A to EA, where E is the matrix E = (0 1 1 0). (a) Write down the coordinate vector [C]_s of the matrix C = (1 3 2 4) with respect to B (b) Find the matrix [T]_B representing T in the basis B (c) Verify the equality [T (C)]_B = [T]_B [C]_B (d) Find the eigenvalues of T and bases of the corresponding eigenspaces (e) Find all solutions of the equation EA = lambda A, with A Elementof M_2, 2 and lambda Elementof R
Show transcribed image text Let M_2, 2 be the vector space of all 2 times 2 matrices with real entries. This has a basis given by B = {(1 1 1 1), (0 0 1 0), (0 1 0 0), (0 0 1 0), (0 0 0 1)} Consider the linear transformation T: M_2, 2 rightarrow M_2, 2 sending a matrix A to EA, where E is the matrix E = (0 1 1 0). (a) Write down the coordinate vector [C]_s of the matrix C = (1 3 2 4) with respect to B (b) Find the matrix [T]_B representing T in the basis B (c) Verify the equality [T (C)]_B = [T]_B [C]_B (d) Find the eigenvalues of T and bases of the corresponding eigenspaces (e) Find all solutions of the equation EA = lambda A, with A Elementof M_2, 2 and lambda Elementof R