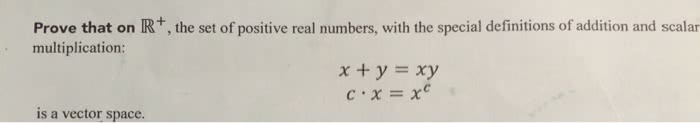MATH 4377 Lecture Notes - Lecture 2: Empty Set, Euclidean Vector, Invertible Matrix
Document Summary
1. 3: subspaces with the operations of addition and scalar multiplication defined. Remark: it"s not as big a pain as you might think to prove that a. Definition: a subset (cid:1849) of a vector space (cid:1848) over a field is called a subspace of (cid:1848) if and only if (cid:1849) is a vector space over on (cid:1848). Several vector space properties are automatically satisfied (vs2), (vs5), (vs6), (vs7) and (vs8) will automatically. We only have to prove only if. It turns out that (4) follows automatically from (2) since the additive inverse of any vector (cid:1875) in (cid:1848) is (cid:4666) (cid:883)(cid:4667)(cid:1875). Theorem 1. 3: let (cid:1848) be a vector space over a field , and suppose (cid:1849) is a subset of (cid:1848). Then (cid:1849) is a subspace of (cid:1848) if and. The zero vector in (cid:1848) is in (cid:1849). (cid:1849) is closed under vector addition inherited from (cid:1848). i. e. if (cid:1876),(cid:1877) (cid:1849), then (cid:1876)+(cid:1877) (cid:1849).