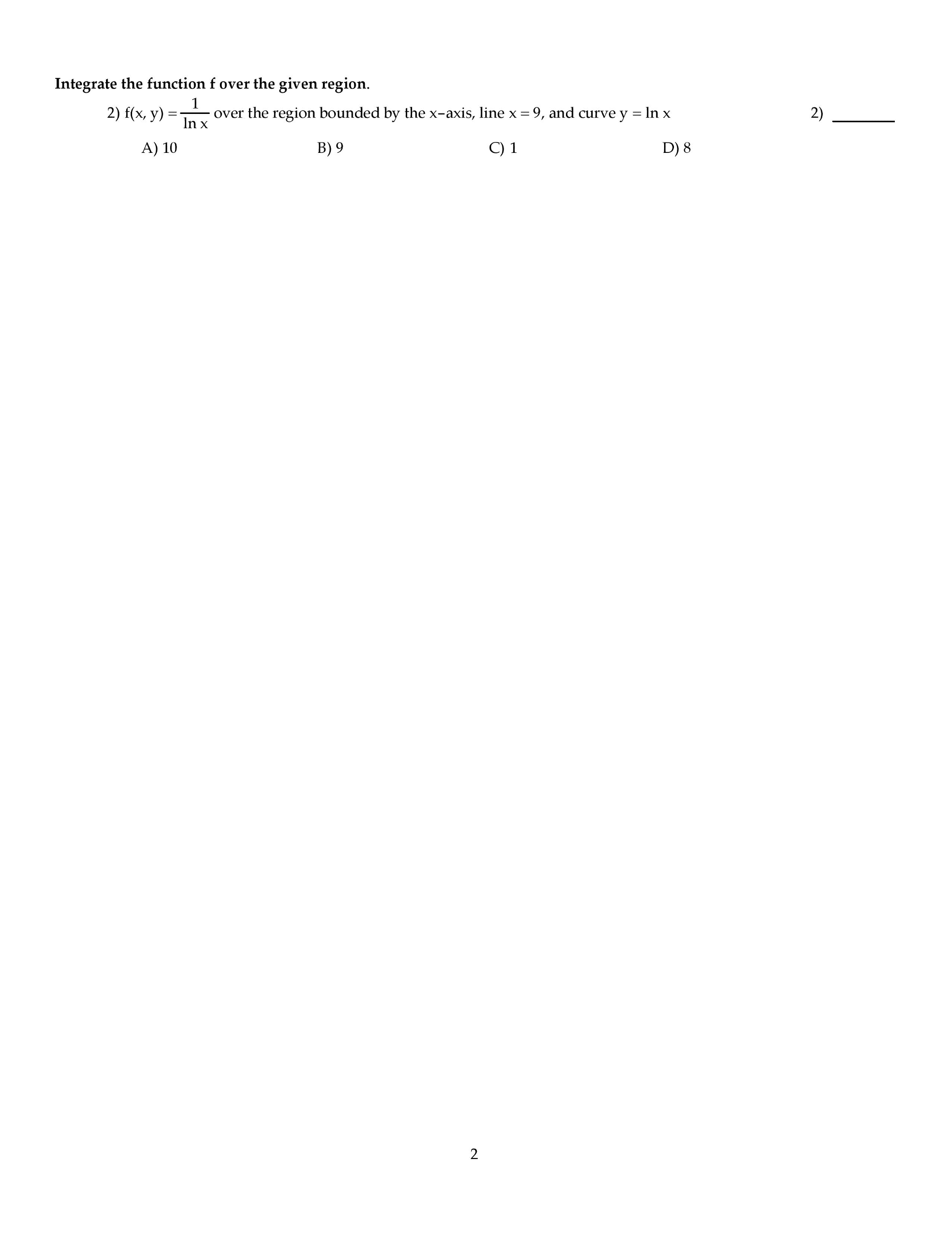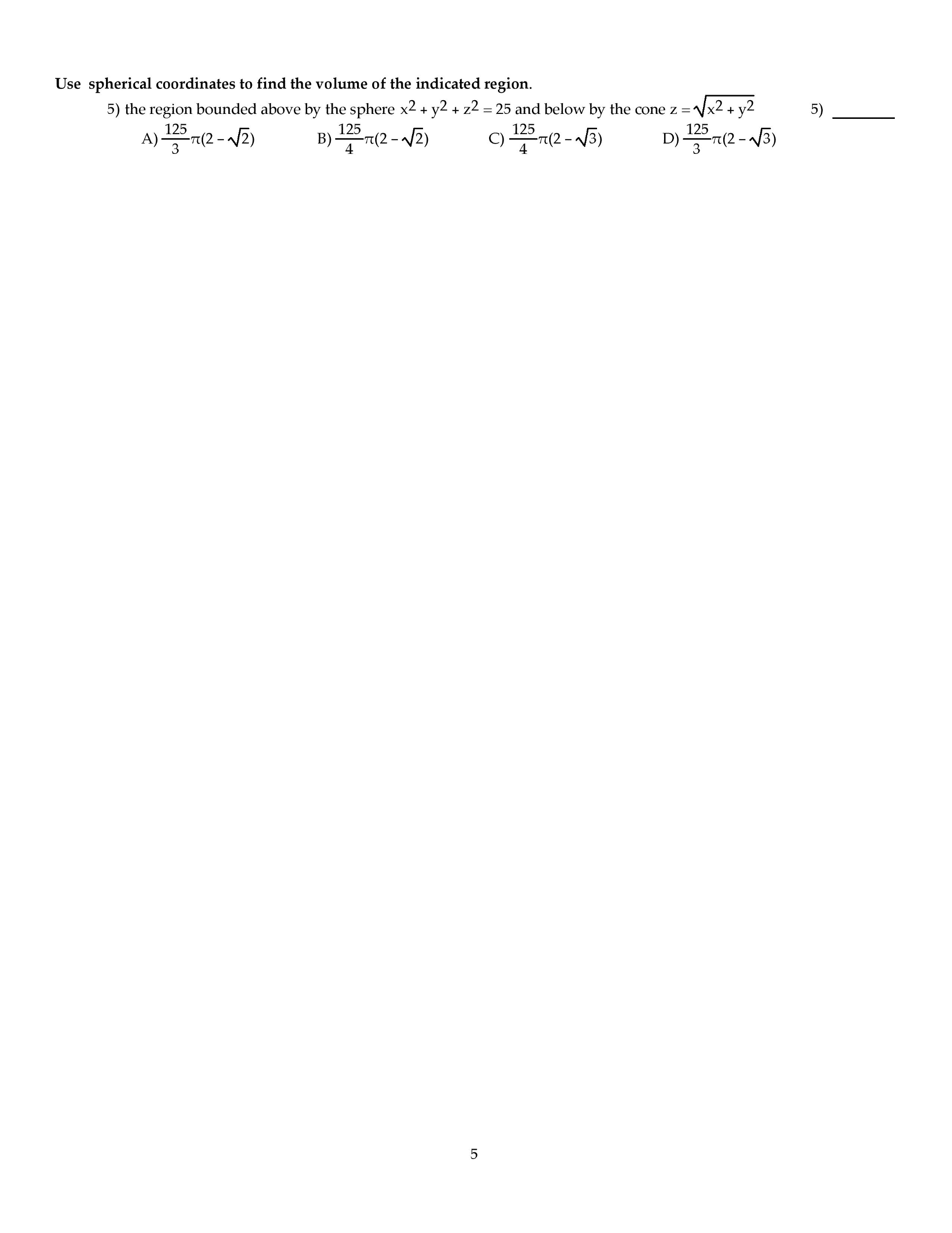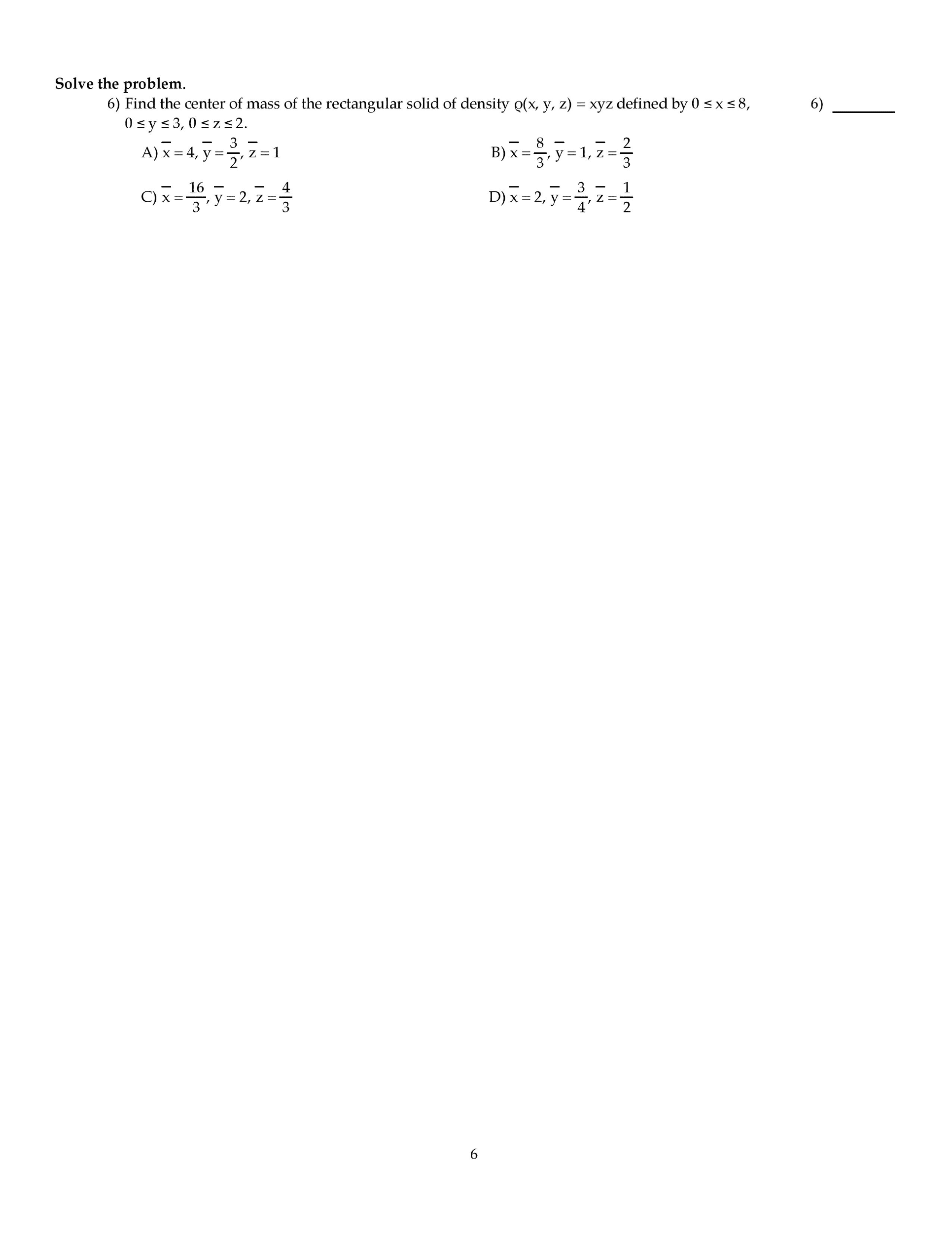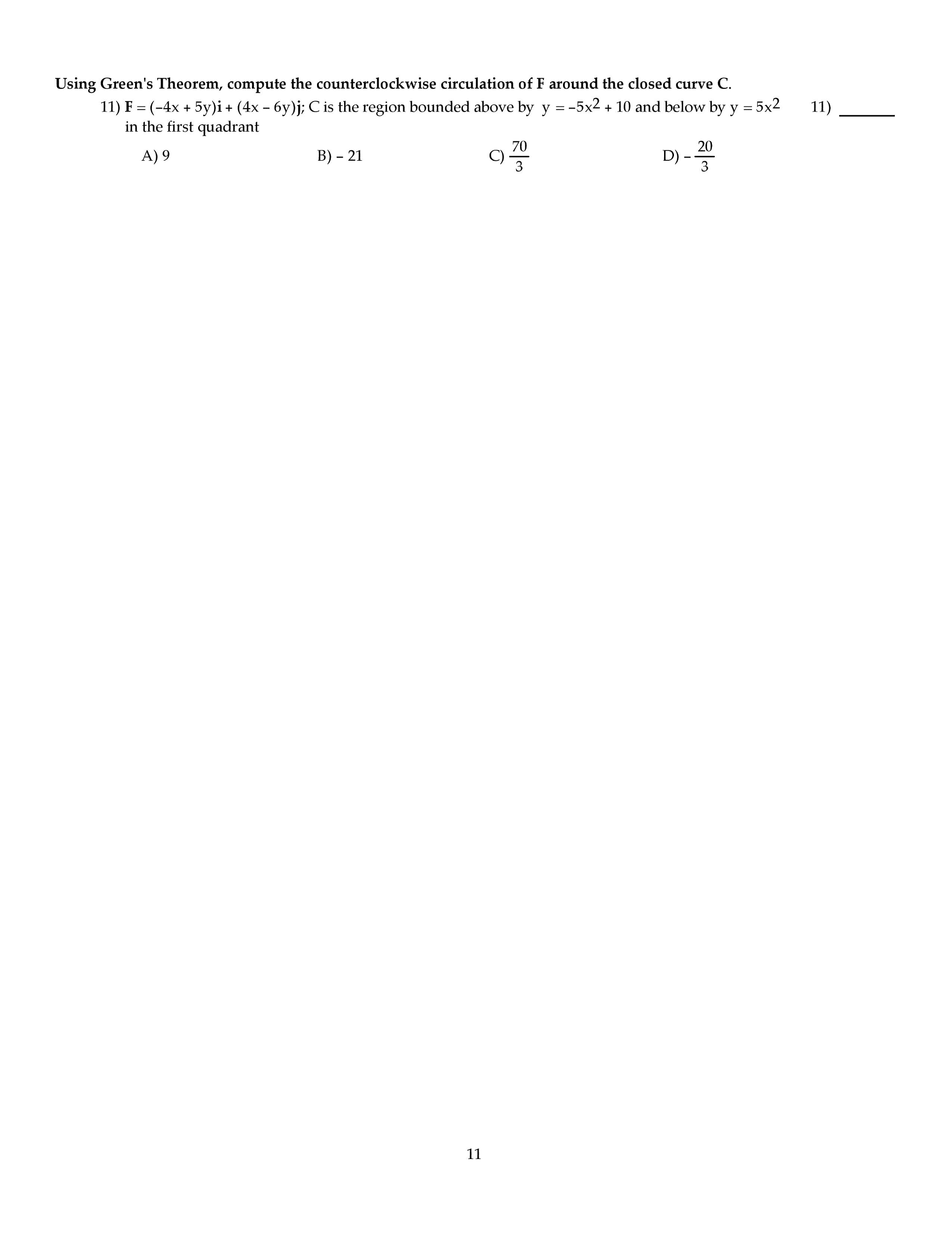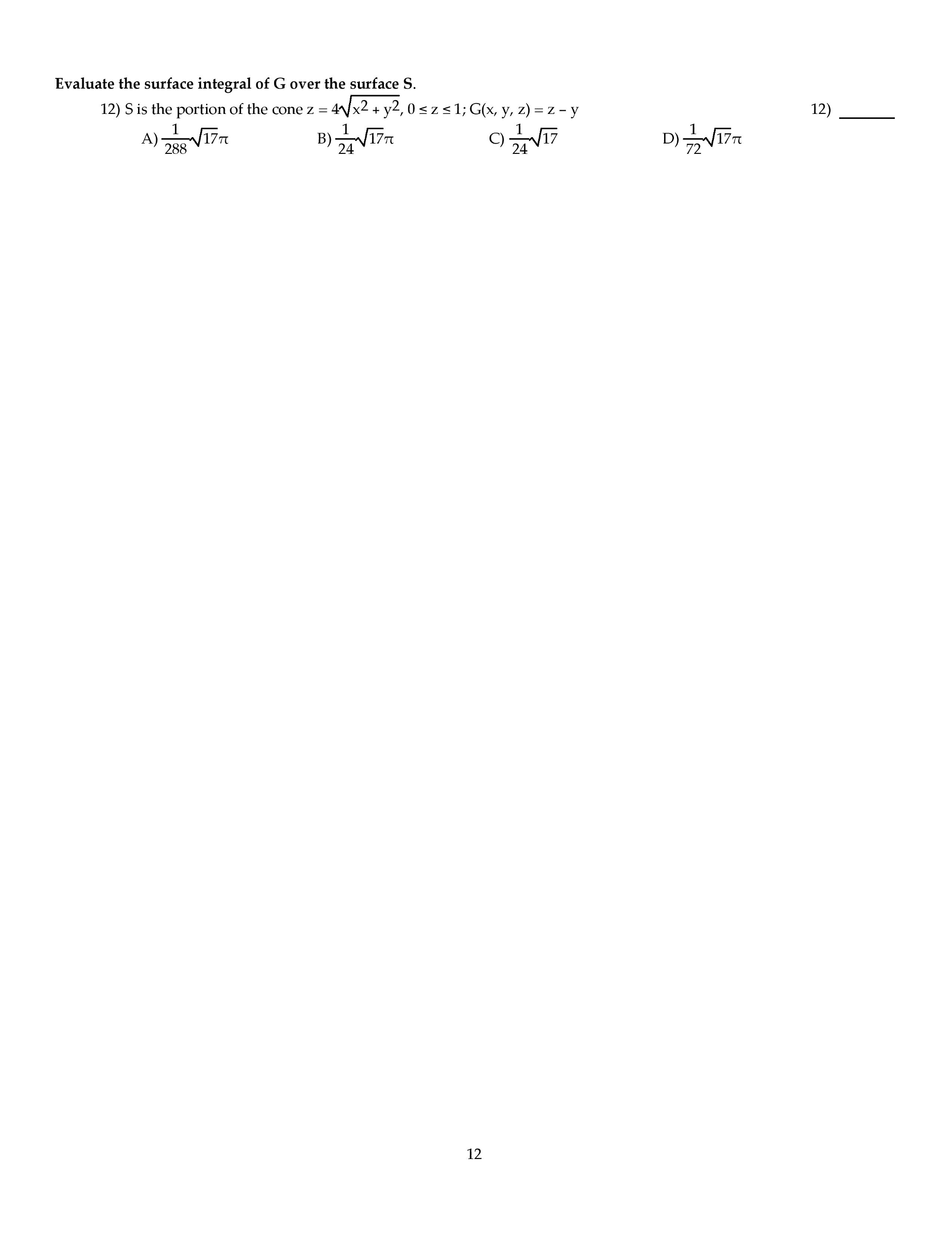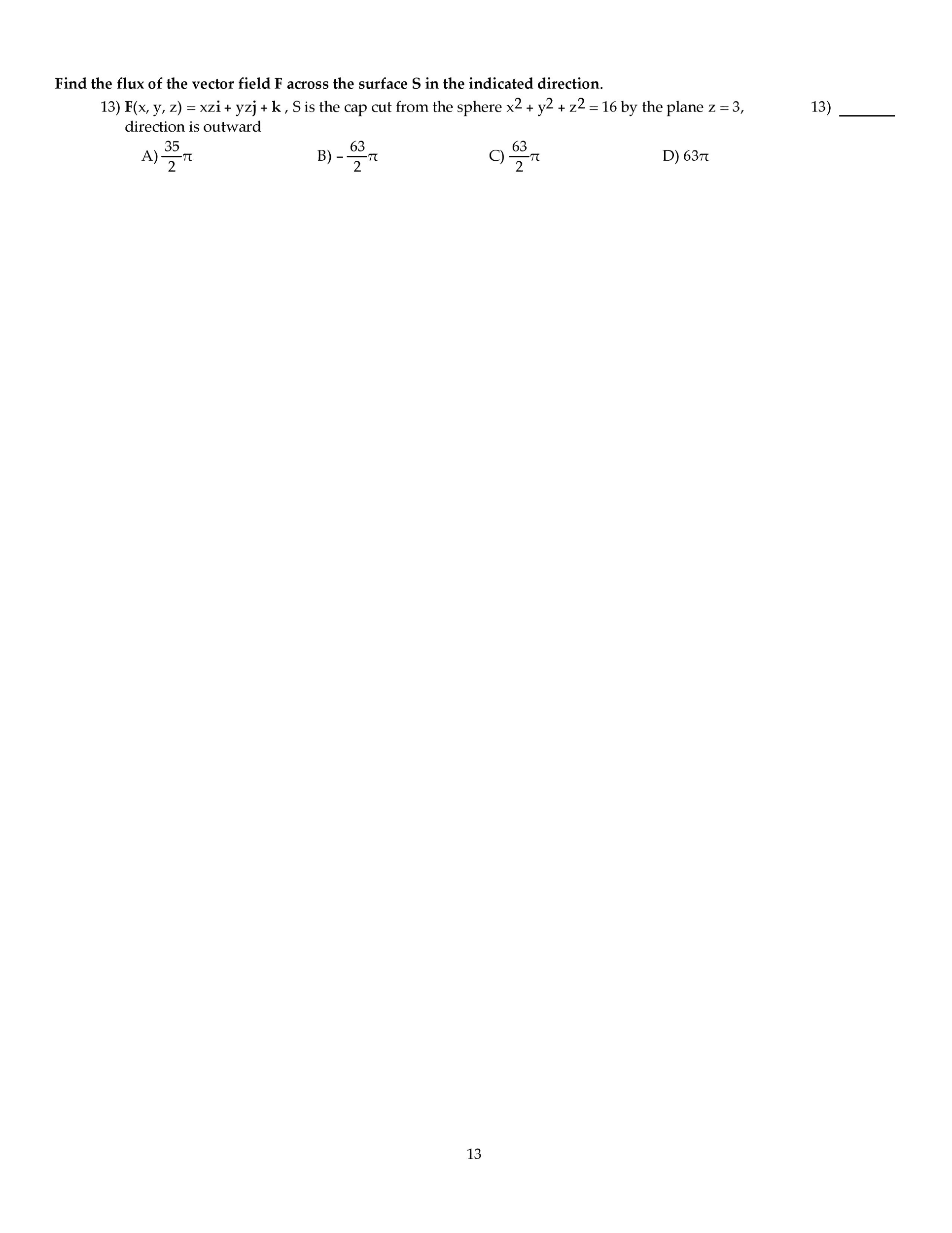L24 Math 233 Lecture Notes - Lecture 28: Cartesian Coordinate System, Multiple Integral, Iterated Integral
L24 Math 233 verified notes
28/45View all
27

L24 Math 233 Lecture Notes - Lecture 27: Glossary Of Arithmetic And Diophantine Geometry, Iterated Integral, Nissan L Engine
28

L24 Math 233 Lecture Notes - Lecture 28: Cartesian Coordinate System, Multiple Integral, Iterated Integral
29

L24 Math 233 Lecture Notes - Lecture 29: Iterated Integral, Polar Coordinate System, Nissan L Engine
Document Summary
To convert between rectangular and polar coordinates, use these equations not (x,y) r, cos sin x = r y = r. R2 = x2 + y2 an t y. D = { r 1 2 r2 d . D = { x2 + y2 4 y. Note: d is a the polar rectangle 1. { r 2 . + 4 2 y = 3 + 4 2 y (x, ) x f rcos . 2 solve from there like in the previous example. , 0 looks like a spiral, centered at (0,0) 0 2 a circle centered at (1,0) 0 fan-shaped, centered at (0,0) Theorem: curve for r = c os is a circle of radius r = 2. To prove this, convert to rectangular coordinates. Describe d for right lobe of fan shaped polar graph. Idea: look at the top curve and the bottom durve to get.