MTH 101 Study Guide - Final Guide: Pythagorean Theorem, Level Set

87 views2 pages

tanscorpion22

18 Jun 2021

School

Department

Course

Professor

For unlimited access to Study Guides, a Grade+ subscription is required.

Document Summary

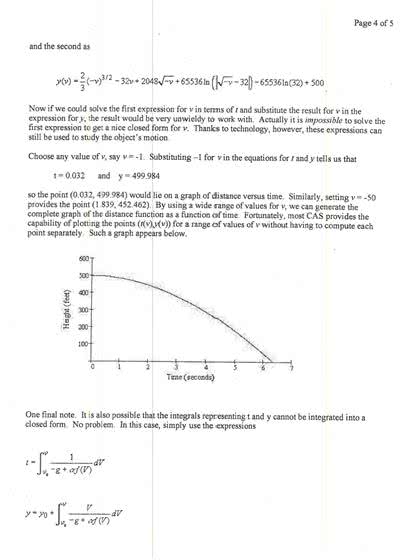
Spring 2021: answer: let v(t) be the velocity vector of the particle. Since v(t) v(t) = kv(t)k2 and the speed kv(t)k is assumed to be constant, we can di erentiate both sides to obtain. 2(v(t) v (t)) = 0 or simply v(t) v (t) = 0. i. e. , the velocity vector and the acceleration vector are orthogonal: answer: let a(t) be the acceleration vector. Then: (r(t) v(t)) = r (t) v(t) + r(t) v (t) + r(t) a(t) = r(t) a(t) 1 + 4a2t2 (d) answer: recall that t and n are always orthogonal. Hence, by the pythagorean theorem, or (recall that an (t) 0 always. ) Hence, kr (t)k = at (t)2 + an (t)2 an (t) = pkr (t)k2 at (t)2. an (t) = s(2a)2 (cid:18) Spring 2021 (e) answer: using the fact kr (t)k = 1 + 4a2t2, we obtain.

Related Questions

Page 3 of 5 which gives us y as a function of Theoretically. the integration on the right of t= 1/ - g + alpha f(V)dv can be performed and the result could provide velocity. v,. as a function of t; Then we could perform the integration in y=y0 + V/- g + alpha f(V)dv and substitute v(t) to obtain y as a function of t. Theoretically, that is. Let's look at in example An Example Suppose the air resistance model for a particular object in free fall has where units for v area feet/second Note how f is defined in terms of the sign of v. As usual. downward has been selected as the negative direction so velocities v of an object in free fall will have negative values Thus -v will be positive and the square root makes. sense Similarly if the object is moving upward, v> 0. the value of f(v)) is negative. The object is dropped from a height: of 500 feet with no initial velocity Using g = 32, the integral models from above becomes and where we have used the definition of f(v) for negative values of v since the object is in free fall With a little hard work or the use of a CAS, the first equation can be written as Page 4 of 5 and the second as Now if we could solve the first expression for v in terms of r and substitute the result for v in the expression for y, the result would be very unwieldy to work with. Actually it is impossible to solve the first expression to get a nice closed form for v. Thanks to technology. however, these expressions can still be used to study the object's motion Choose any value of v. say v=-1. Substituting -1 for v in the equations for t and y tells us that t = 0.032 and y = 499.984 so the point (0.032, 499.984) would lie on a graph of distance versus time Similarly, setting v = -50 provides the point (1 839, 452 462) By using a wide range of values for v. we can generate the complete graph of the distance function as a function of time Fortunately, most CAS provides the capability of plotting the points (t(v), y(v)) foe a range of values of v without having to compute each point separately Such a graph appears below. One final note. It is also possible that the integrals representing t and y cannot be integrated into a closed form No problem In this case, simply use the expressions t= 1/ - g + alpha f(V)dV y=y0+ V/ - g + alpha f(V)dV Page 5 of 5 and the numerical integrators provided by a CAS to determine values of t und y Exercises In all of the exercises you will need a CAS or related tool In the example above the graph indicates the object strikes the ground some time between 6 and 7 seconds from release Determine this time to three decimal places In the case where alpha = 1/2 ,f(v) = -v, v0 = 0, y0=100 determine closed form. expressions for v and y as function. Of t. An object is thrown upward at 40 ft/sec from a height of 100 feet The air resistance can be modeled by alpha =0.001 and f(v) = - |v| v Using the trajectory model determine the speed of the object when it strike the ground, determine the time the object strikes the ground after takeoff, construct the graph of the object's height versus time.

Please help fill in the rest of the blanks.

MTH 101 Study Guide - Final Guide: Pythagorean Theorem, Level Set

Document Summary

Get access

Related Documents

MTH 101 Final: dis 3

MTH 101 Study Guide - Final Guide: Quotient Rule, Cartesian Coordinate System

MTH 101 Study Guide - Final Guide: Parallelepiped, Vector Projection

Related Questions