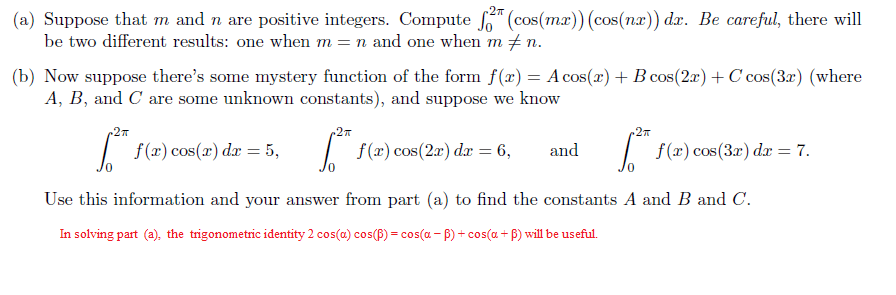1
answer
0
watching
124
views
13 Nov 2019
(a) Use the product formula sin mx cos nx =1/2[sin(m+n)x +sin(m-n)x] to show that 2sin (x/2) cos kx=sin(k+(1/2))x - sin(k-(1/2))x
(b)Add the identities in part (a) for k=1,2,...,n and exploit cancellations to get a formula [sigma notation of cos kx = (sin(n+(1/2))x - sin(x/2))/2sin(x/2) ]where x is not an integer multiple of 2pi
(c)Use the product formula in (a) again to write the sum in (b) in a different form sigma notation of cos kx=[ sin (nx/2) cos (1/2)(n+1)x]/sin (x/2)
(a) Use the product formula sin mx cos nx =1/2[sin(m+n)x +sin(m-n)x] to show that 2sin (x/2) cos kx=sin(k+(1/2))x - sin(k-(1/2))x
(b)Add the identities in part (a) for k=1,2,...,n and exploit cancellations to get a formula [sigma notation of cos kx = (sin(n+(1/2))x - sin(x/2))/2sin(x/2) ]where x is not an integer multiple of 2pi
(c)Use the product formula in (a) again to write the sum in (b) in a different form sigma notation of cos kx=[ sin (nx/2) cos (1/2)(n+1)x]/sin (x/2)
1
answer
0
watching
124
views
For unlimited access to Homework Help, a Homework+ subscription is required.
Jean KeelingLv2
13 Nov 2019