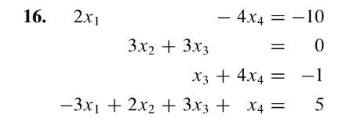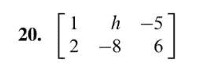MATH 1119 Final: Math 1119 Final Review
19 Sep 2015
School
Department
Course
Professor
Document Summary
Section 1. 1 systems of linear equations: a linear equation is an equation that can be write in this form: 3: consistent : at least one solution ( one solution or infinitely many solutions) 3: equality of vector: two vectors u and v are said to be equal, that is u = v, if and only if they have the same number of entries and their corresponding entries are equal. Matrix equation: the equation ax = b has a solution if and only if b can be written as a linear combination of the columns of a. Then the following four statements are logically equivalent. a) for each b in rm, the equation ax = b has a solution. b)each b in rm is a linear combination of the columns of a. c) the columns of a span rm . d) a has a pivot position in every row.
