Published on 20 Nov 2012
School
Department
Course
Professor
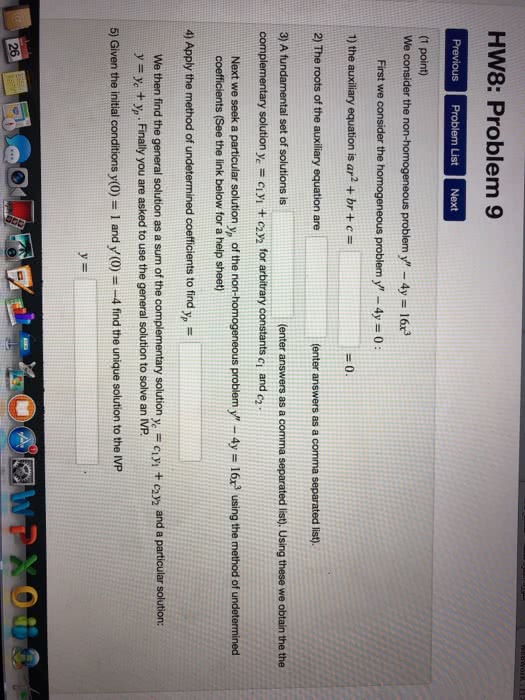
Quiz 3a Solutions
1. This question concerns second-order linear homogeneous equations. Show your
work.
(a) Find two linearly independent solutions of y′′ + 6y′+ 9y= 0.
The characteristic equation is r2+ 6r+ 9 = 0, which factors as (r+ 3)2= 0,
so there is a double root r=−3. Thus two linearly independent solutions
are given by
y1=e−3x, y2=xe−3x
(b) Find the general solution of y′′ + 4y= 0.The characteristic equation
is r2+ 4 = 0, with complex conjugate roots r=±2i. Thus two linearly
independent solutions are given by
y1= cos 2x , y2= sin 2x
and the general solution is
y=c1y1+c2y2
=c1cos 2x+c2sin 2x
2. The solution of x′′ + 4x= 0, with initial conditions x(0) = 1,x′(0) = −2, is
x(t) = cos ω0t−sin ω0t
where I haven’t told you what ω0is, but we can figure it out.
(a) What is ω0?
We might remember that the differential equation is in the form x′′ +ω2
0x= 0,
thus ω0= 2. Or we might observe that x′′ =−ω2
0cos ω0t+ω2
0sin ω0t, and
since this is a solution of x′′ + 4x= 0, we must have ω2
0= 4, thus ω0= 2.
(b) Find numbers C,αsuch that x(t)is written x(t) = Ccos(ω0t−α). (Hint:
we must have Ccos α= 1,Csin α=−1; drawing the unit circle may help
you.)
We must find C,αsuch that Ccos α= 1, Csin α=−1. Thus C=
p
12+ (−1)2=
√
2. Since cos α > 0 and sin α < 0, the angle αis in
the fourth quadrant, with tan α= sin α/ cos α=−1, thus α= 7π/4. So
x(t) =
√
2 cos(2t−7π/4)
1