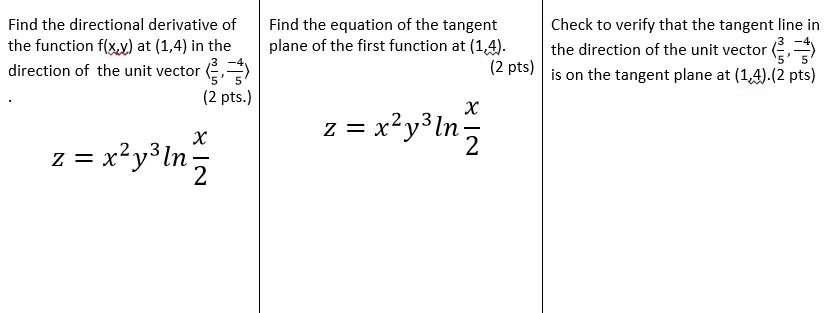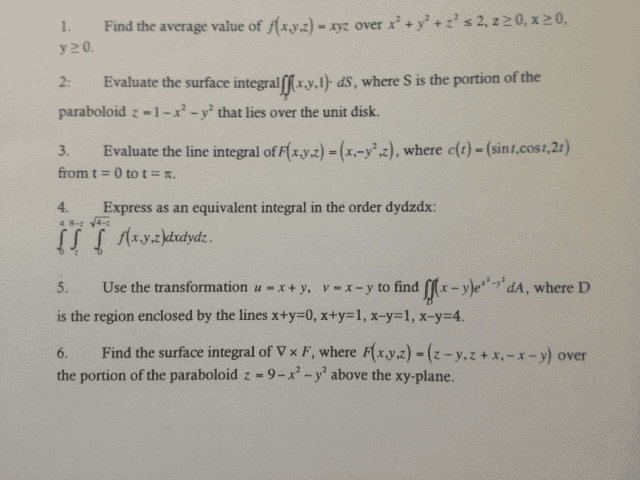MATH 200 Study Guide - Quiz Guide: Tangent Space, Directional Derivative

MATH 200 104 Quiz 3
First Name: Last Name: Student Number:
1. (5 points) Consider the function f(x, y) = x2y3where x(s, t) = es−tand y(s, t) = 3s−t.
∂f
∂t
(s,t)=(1,1) =-28
When (s, t) = (1,1) we have x(1,1) = e0= 1 and y(1,1) = 2.
∂f
∂t =∂f
∂x
∂x
∂t +∂f
∂y
∂y
∂t
= (2xy3) (−es−t) + (3x2y2) (−1)
= (2 ·1·23) (−e1−1) + (3 ·12·22) (−1)
= (16) (−1) + (12) (−1)
=−28
2. (3 points) For f(x, y) = x
y2find the following at (4,2).
The tangent line at (4,2) parallel to the xy-plane: ~r(t) = h4t+ 4, t + 2,1i
Since the form of the line was not specified there are many solutions to this problem.
Solution 1: Because this line is horizontal to the tangent plane it has directional vector
~m =ha, b, 0i. Also, ~v =ha, biis the direction at which the directional derivative is 0 (i.e. ~v is
perpendicular to the gradient vector.)
Of=h1
y2,−2x
y3i
Of(4,2) = h1
4,−1i
Of(4,2) ·~v = 0
h1
4,−1i·ha, bi= 0
a
4−b= 0
This has many solutions including a= 4 and b= 1 so let ~v =h4,1i.
Our solution is the line with directional vector ~m =h4,1,0ithrough the point (4,2,1).
Solution 2: In this solution we will intersect the tangent plane with the horizontal plane
z= 1 through the point (4,2,1). Same as above Of(4,2) = h1
4,−1i, so the normal vector is
~n =h1
4,−1,−1i.
The tangent plane is 1
4(x−4) −(y−2) −(z−1) = 0
The intersection of 1
4(x−4) −(y−2) −(z−1) = 0 and z= 1.
This is equivalent to
the intersection of 1
4(x−4) −(y−2) = 0 and z= 1.
1

51
MATH 200 Full Course Notes
Verified Note
51 documents
Document Summary
Student number: (5 points) consider the function f (x, y) = x2y3 where x(s, t) = es t and y(s, t) = 3s t. When (s, t) = (1, 1) we have x(1, 1) = e0 = 1 and y(1, 1) = 2. = (2 1 23) ( e1 1) + (3 12 22) ( 1) = 28: (3 points) for f (x, y) = x y2 nd the following at (4, 2). The tangent line at (4, 2) parallel to the xy-plane: ~r(t) = h4t + 4, t + 2, 1i. Since the form of the line was not speci ed there are many solutions to this problem. Solution 1: because this line is horizontal to the tangent plane it has directional vector. Also, ~v = ha, bi is the direction at which the directional derivative is 0 (i. e. ~v is perpendicular to the gradient vector. ) F (4, 2) ~v = 0 h.