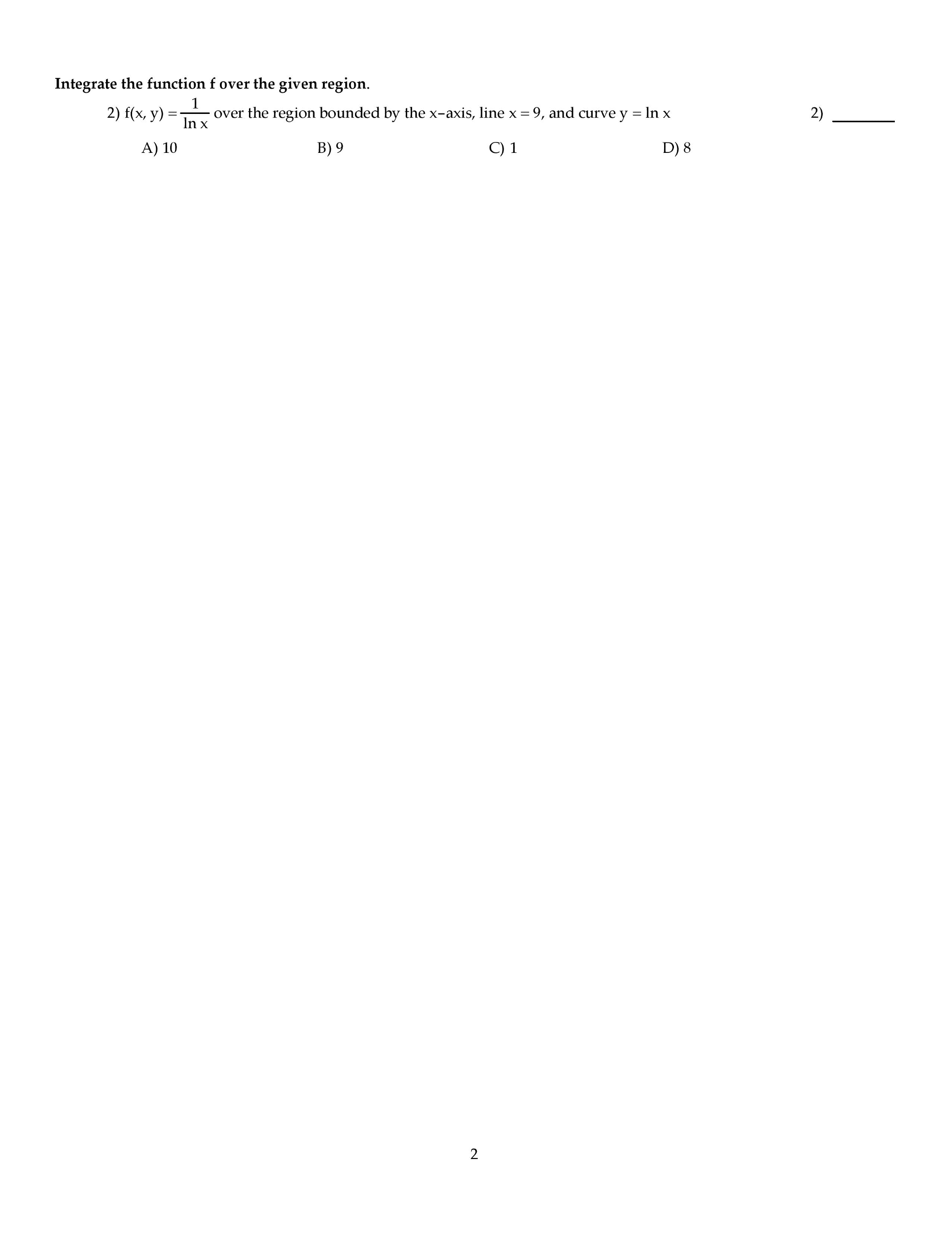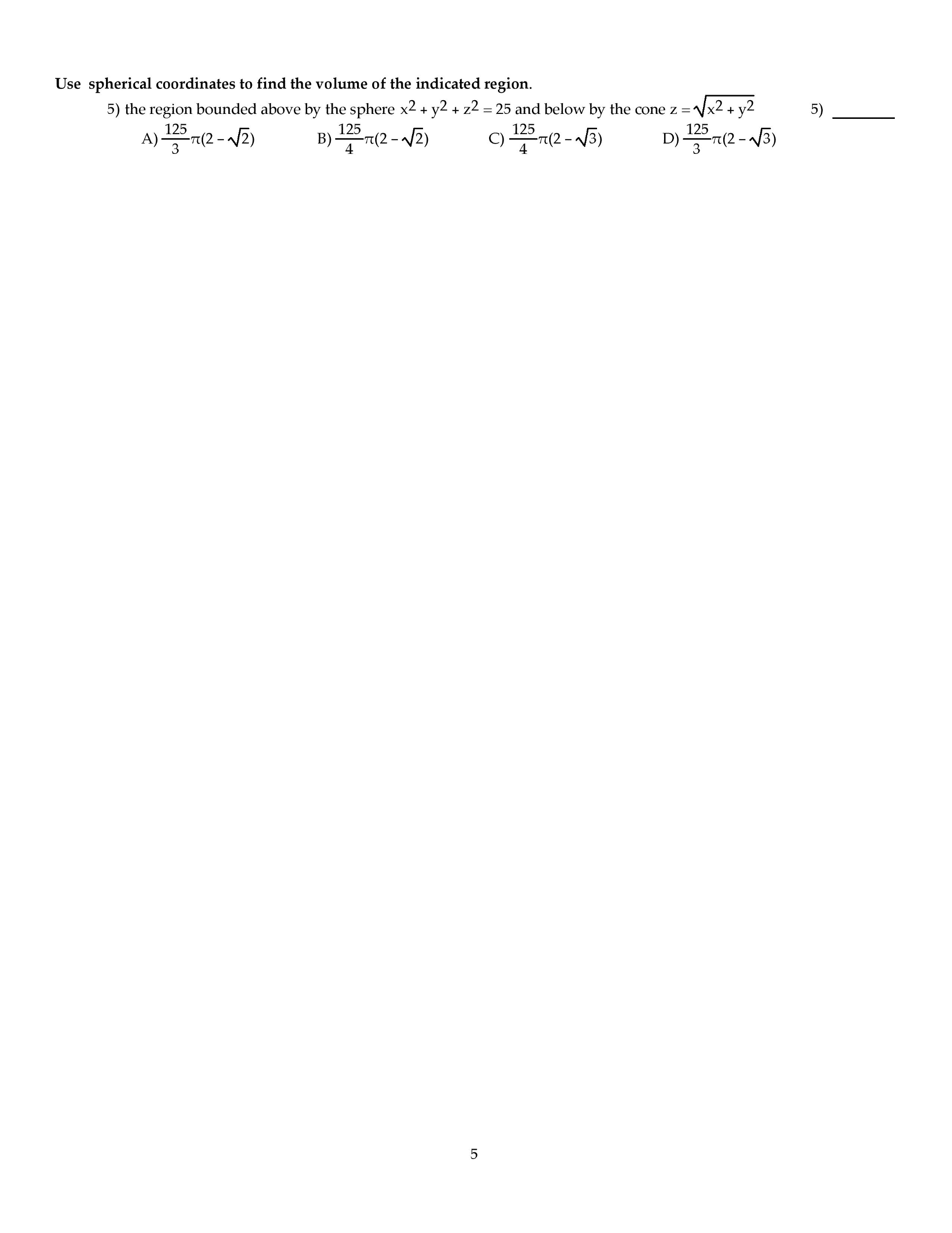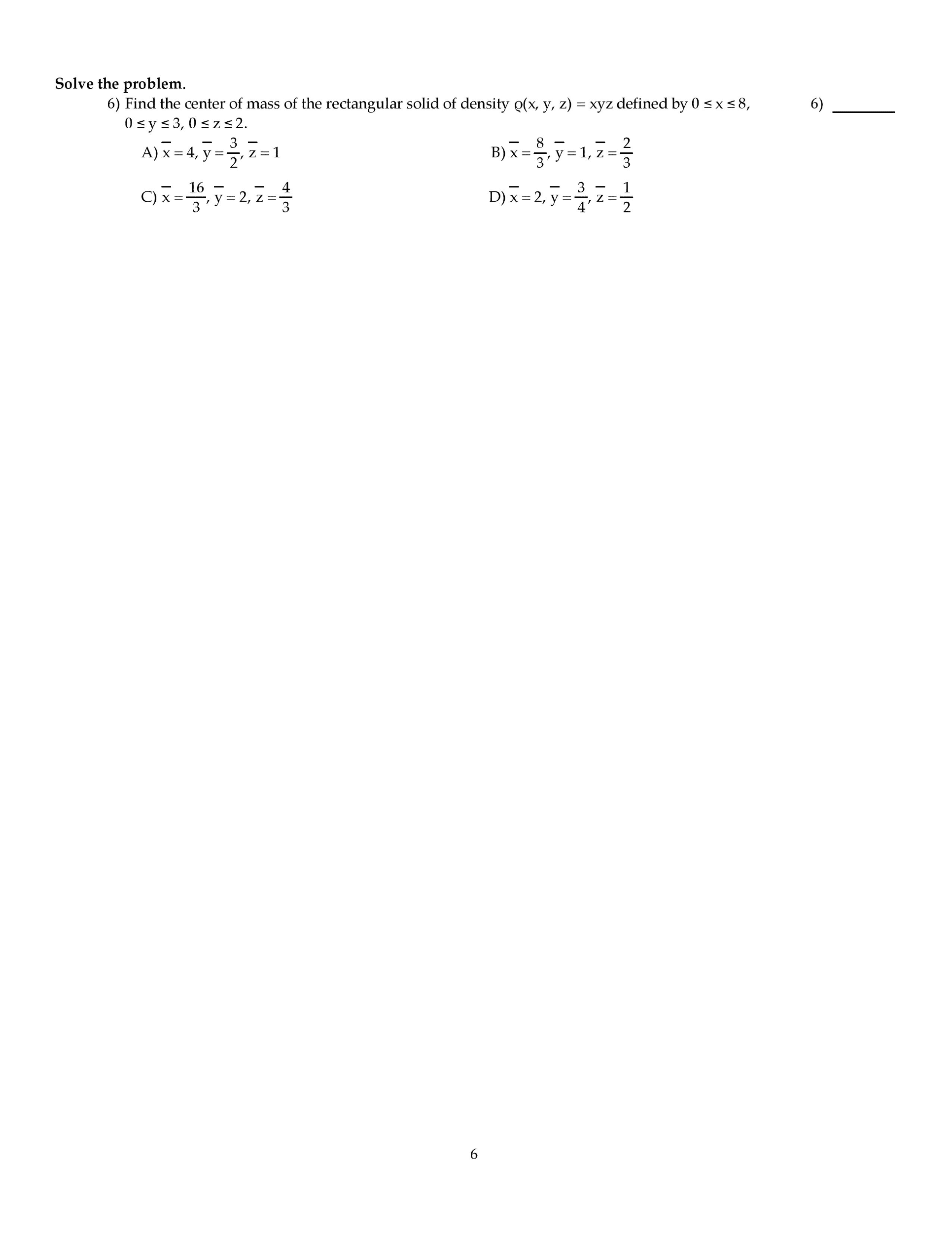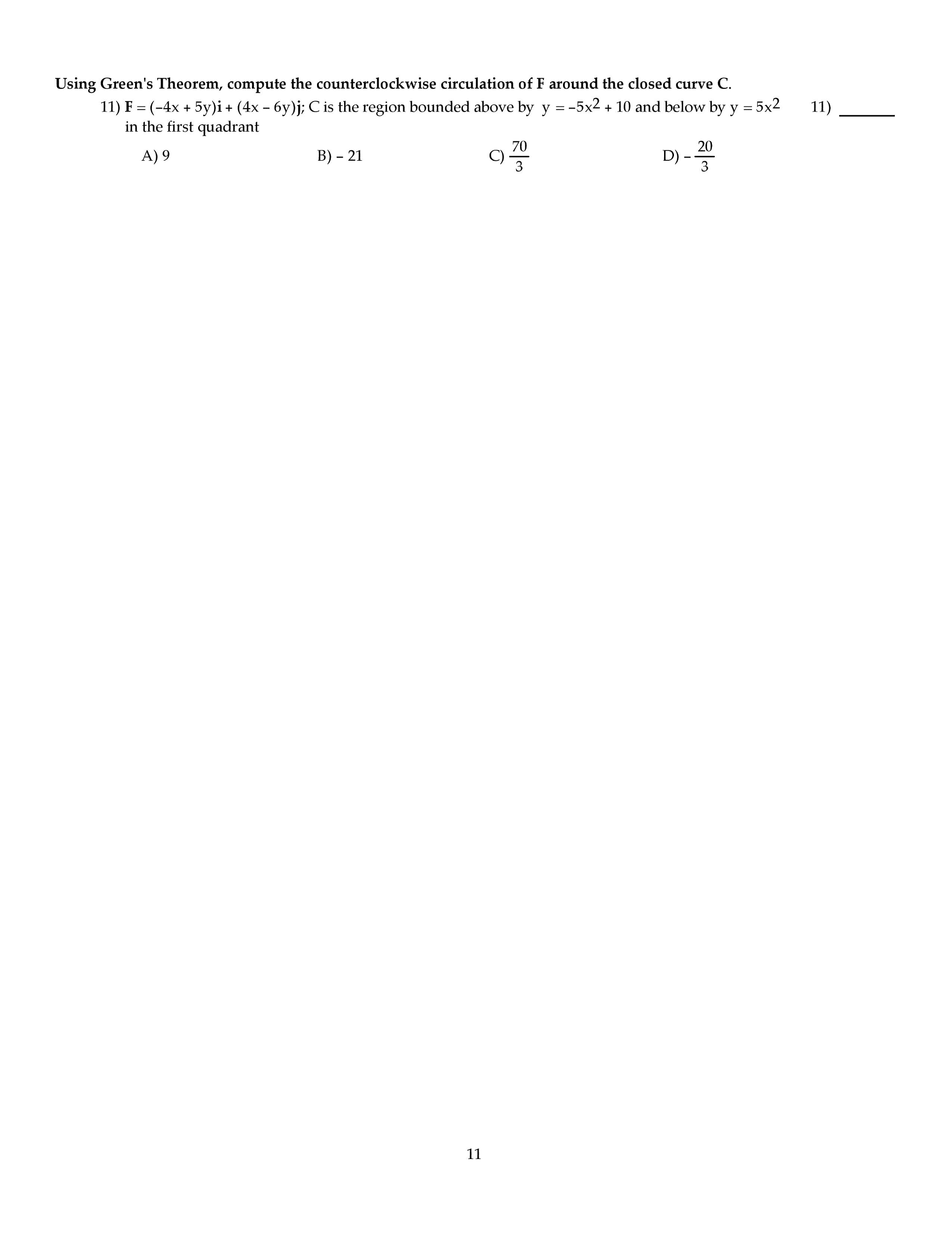MATH1003 Midterm: MATH 1003 UNB Exam 1003 06
Document Summary
May 11: (10 points) (a) (5 points) the point (1, 1) is an intersection of the graphs of y = x and y = x4. Compute the curvature of of the curve c at (1, 1. Hint: write down a parametrization ~r(t) of c rst. 0 (x2 + y2)2 if (x, y) 6= (0, 0), if (x, y) = (0, 0). Explain: (10 points) (a) (7 points) use the lagrange multiplier method to nd the absolute maximum and minimum values of the function f (x, y) = xy 1 subject to the constraint x2+y2 = 2. 0 f (x, y, z)dxdydz: (10 points) Hint: compute i 2 rst. (a) (5 points) let i = r (b) (5 points) use spherical coordinates to compute zzze dx. ~f d~r where ~f = hey2z, 2xyzey2z, xy2ey2zi and c is the polygonal line segment from (0, 0, 0) to (1, 0, 0) and then from (1, 0, 0) to (1, 1, 1).