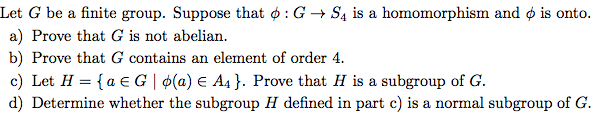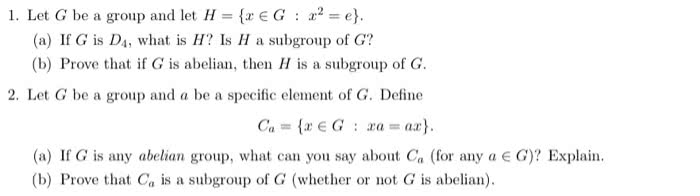These questions are asking about subrgoups, groups, isormorphic.
actually, after 2day, I got a midterm for abstract math test,and I got a sample of midterm test, so I hope to get a solution ofall these question. I think it is a lot, but I hope that pleaseshow me the answer and I want to know why these answer is this.
The reason why these problems are bunch of questions, so I willgive big pts for this questions. thanks.
you guys can upload by the picture.
(below question)
SAMPLE MIDTERM 1, MATH 120A
(1) 1. Write the denition of group.
2. Give an example of a group of order 2011.
3. Give an example of a non-abelian group with 12 elements.
(2) Let (G,*) and (H . ) be groups.
1. Dene what it means for G and H to be isomorphic.
2. Assume that G has exactly two solutions to the equation x^2 =e.
Prove, directly from the denition in (1), that if G and H areiso-
morphic, then H has exactly two solutions to the equation x^2 =e.
3. Prove or disprove: (R, +) is isomorphic (R+, . ). Here R+ ={x is subset of R : x>0}.
4. Prove or disprove: (R, +) is isomorphic (R*, . ). Here R* ={x is subset of R : x is not 0}
(3) Let G be the group Z_20, with addition modulo 20.
1. Draw the subgroup diagram of G, giving a generator for eachsubgroup
2. Find the subgroup H =< 16 > of G.
3. Find a subgroup K of U_20 isomorphic to H.
(4) Let (G, . ) be a group and let H be a subgroup of H. Fix anelement a of
G and let K = { aha^-1 : h is subset of H}
1. Prove that K is a subgroup of G.
2. Prove that the map psi : H -> K, h -> aha^-1 isan isomorphism of groups.
(5) Let (G, . ) be a group and let a be an element of G.
1. Dene the order of a.
2. Give an example of an element of order 4 in GL(2,R).
3. Find the order of 16 in Z_20.
These questions are asking about subrgoups, groups, isormorphic . actually, after 2day, I got a midterm for abstract math test, and I got a sample of midterm test, so I hope to get a solution of all these question. I think it is a lot, but I hope that please show me the answer and I want to know why these answer is this. The reason why these problems are bunch of questions, so I will give big pts for this questions. thanks. you guys can upload by the picture. Write the denition of group. Give an example of a group of order 2011. Give an example of a non-abelian group with 12 elements. Let (G,*) and (H . ) be groups. Dene what it means for G and H to be isomorphic. Assume that G has exactly two solutions to the equation x^2 = e. Prove, directly from the denition in (1), that if G and H are iso- morphic, then H has exactly two solutions to the equation x^2 = e. Prove or disprove: (R, +) is isomorphic (R+, . ). Here R+ = {x is subset of R : x>0}. Prove or disprove: (R, +) is isomorphic (R*, . ). Here R* = {x is subset of R : x is not 0} Let G be the group Z_20, with addition modulo 20. Draw the subgroup diagram of G, giving a generator for each subgroup Find the subgroup H = of G. Find a subgroup K of U_20 isomorphic to H. Let (G, . ) be a group and let H be a subgroup of H. Fix an element a of G and let K = { aha^-1 : h is subset of H} Prove that K is a subgroup of G. Prove that the map psi : H -> K, h -> aha^-1 is an isomorphism of groups. Let (G, . ) be a group and let a be an element of G. Dene the order of a. Give an example of an element of order 4 in GL(2,R). Find the order of 16 in Z_20