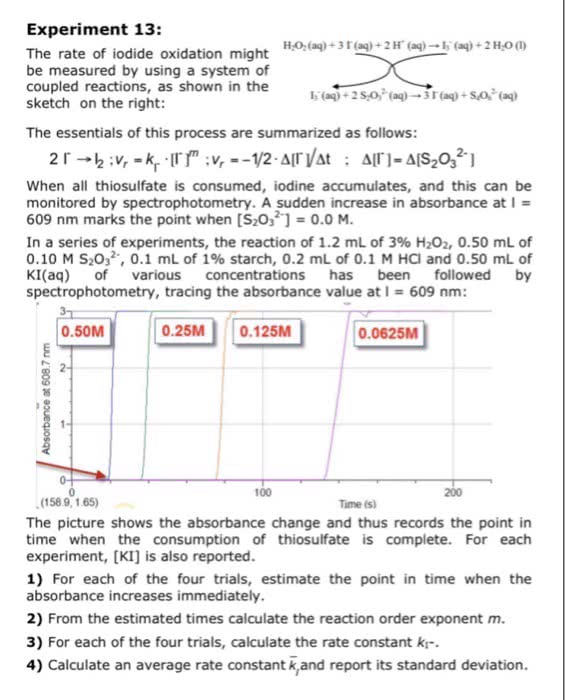
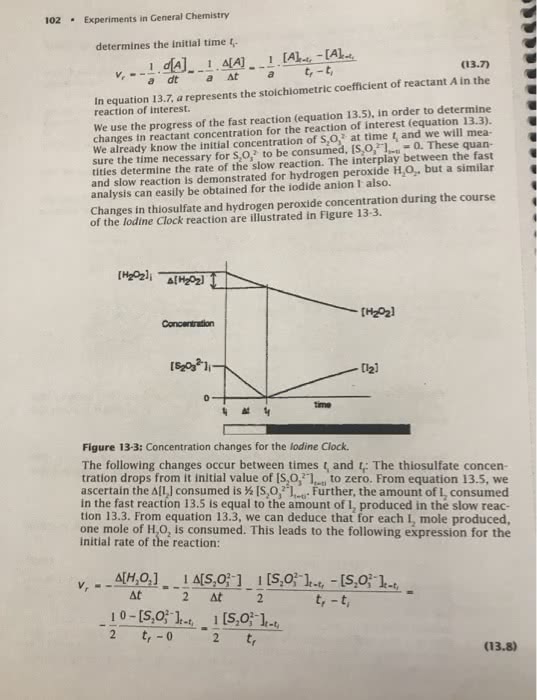
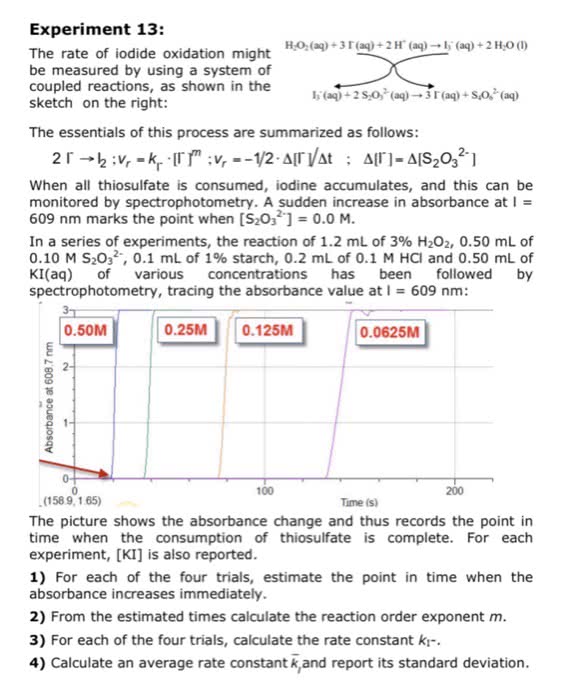
1) Consider the following equation: Rate = k [CH3I]2 [C15H11N]
i) If the concentration of C15H11N is doubled, does the rate constant:
A) Increase
B) Decrease
C) Remain unchanged
ii) If the concentration of of CH3I is decreased by a factor of 3, the time it takes for the reaction to finish will:
A) Increase by a factor of 3
B) Increase by a factor of 9
C) Decrease by a factor of 9
D) Remain Unchanged
iii) If the temperature increases how will the activation energy change:
A) It will increase
B) It will decrease
C) It will remain unchanged
2) During a titration of a weak acid with a strong base you add an additional small amount of base after reaching the equivalence point.
i) How does the pH of the solution change?
A) Increase
B) Decrease
C) Remain unchanged
ii) How does the Ka of the acid change?
A) Increase
B) Decrease
C) Remain unchanged
3) You combine a solution of silver nitrate (AgNO3) and a solution of sodium carbonate (Na2CO3) to form solid silver carbonate (Ag2CO3) and aqueous sodium nitrate (NaNO3), the net ionic equation is listed below. You observe the white solid, Ag2CO3 in the test tube. You add a strong acid (HNO3) to the mixture and it reacts with the carbonate ions as listed in the equations below. What would you expect to observe when adding the strong acid to the test tube?
2 Ag+(aq) + CO32-(aq) <--> Ag2CO3(s)
2 H+(aq) + CO32-(aq) <--> H2CO3
H2CO3 -> H2O(l) + CO2(g)
A) An increase in the amount of white solid
B) A color change of the solid
C) A decrease in the amount of white solid
D) No change in the amount of white solid
4) Ksp of BaF2 at room temperature is 1.84 x 10-7. It is also known that the reaction of dissolution of BaF2 is endothermic. Imagine that you have a saturated solution of BaF2 at equilibrium, that has some undissolved BaF2 precipitated on the bottom of the test tube.
4.1) If the temperature is increased how would that affect:
i) The solubility of BaF2
A) Increase
B) Decrease
C) Remain Unchanged
ii) The solubility constant of BaF2
A) Increase
B) Decrease
C) Remain unchanged
4.2 An additional amount of BaF2 was added to the solution how would that affect:
i) The solubility of BaF2
A) Increase
B) Decrease
C) Remain unchanged
ii) The solubility constant of BaF2
A) Increase
B) Decrease
C) Remain unchanged
4.3 If NaF is added to the solution how will it affect:
i) The solubility of BaF2
A) Increase
B) Decrease
C) Remain Unchanged
ii) The solubility constant of BaF2
A) Increase
B) Decrease
C) Remain unchanged