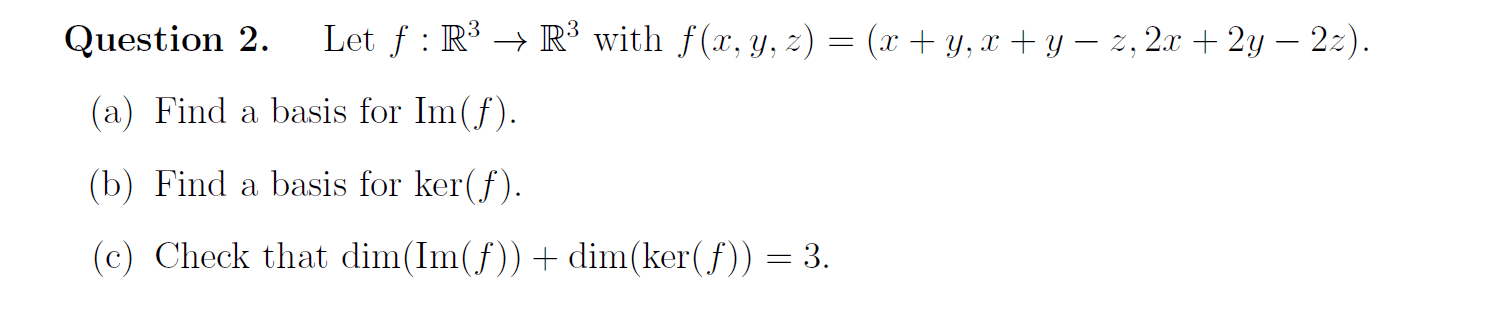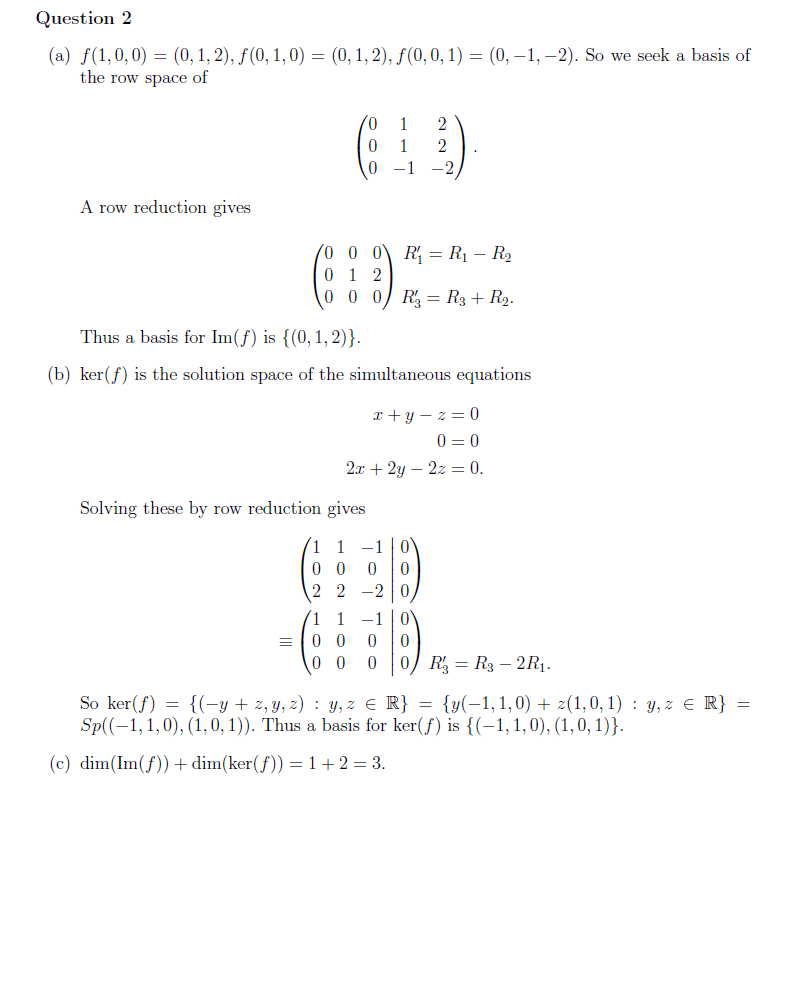Q2
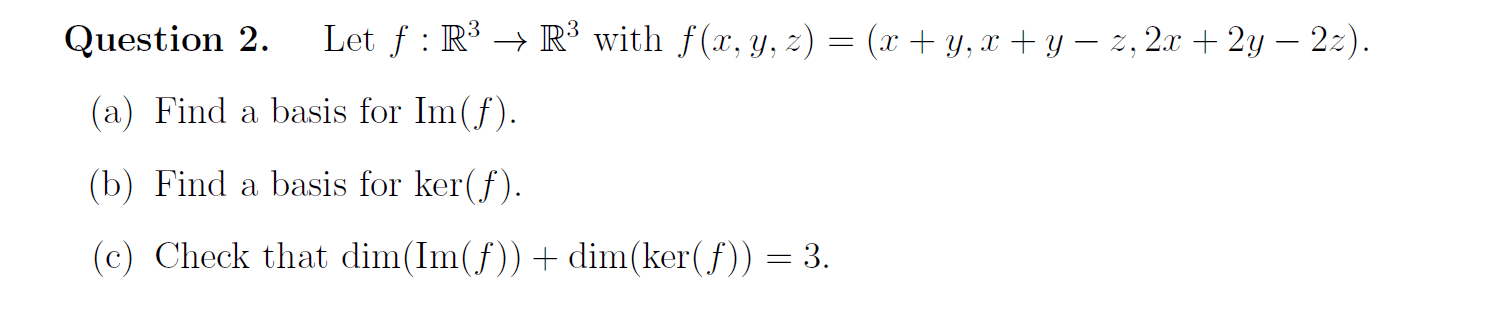
Modle answer but different numbers
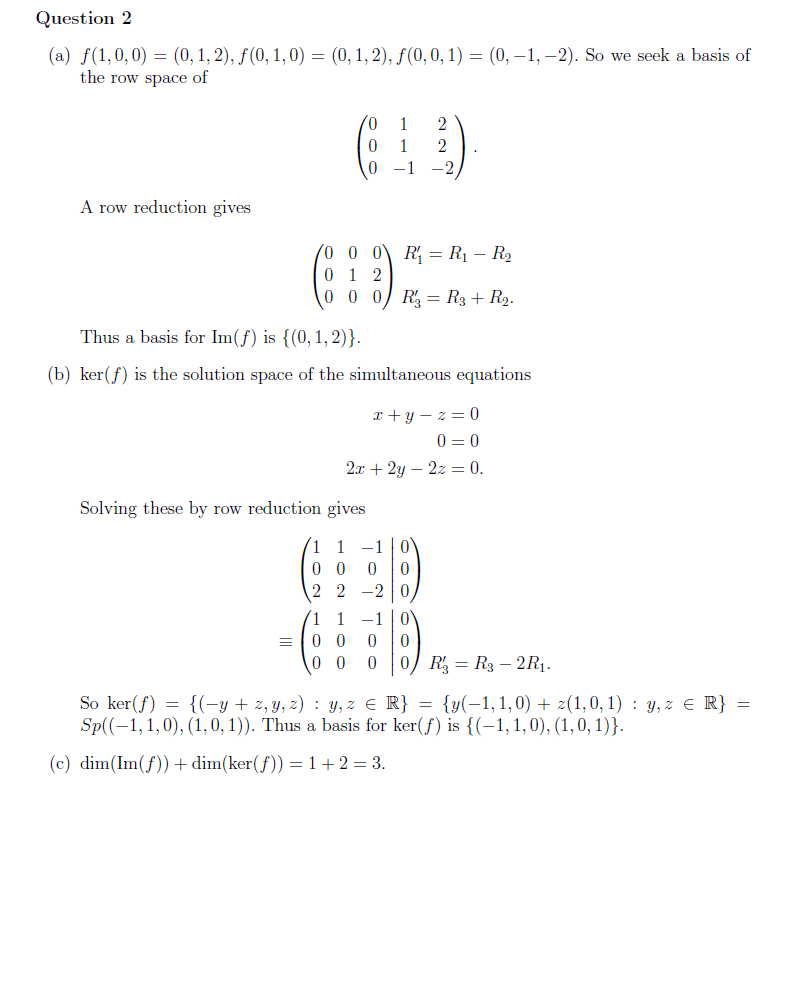
Let f : R3 rightarrow R3 with f(x, y, z) = (= (x + y, x + y - z,2x -h 2y -2z). Find a basis for Im(f). Find a basis for ker(f). Check that dim(Im(f)) + dim(ker(f)) = 3. f(1,0,0) = (0,1.2).f (0,1,0) = (0,l,2),f(0,0,1) = (0,-1,-2). So we seek a basis of the row space of A row reduction gives Thus a basis for Im(f) is {(0,1,2)}. (b) ker(f) is the solution space of the simultaneous equations x + y - z = 0 0 = 0 1x + 2y - 2z+0Solving these by row reduction gives So ker(f) = {(-y + z, y, z) : y, z epsilon R} = {y(-l, 1,0) + z(1,0,1) : y, z epsilon R} = Sp((-1,1,0), (1,0,1)). Thus a basis for ker(f) is {(-1,1,0), (1,0,1)}. (c) dim(Im(f)) + dim(ker(f)) = 1 + 2 = 3.