CHEM 130 Chapter Notes - Chapter 2: Louis De Broglie, Electronic Correlation, Photon
11 Sep 2018
School
Department
Course
Professor
Document Summary
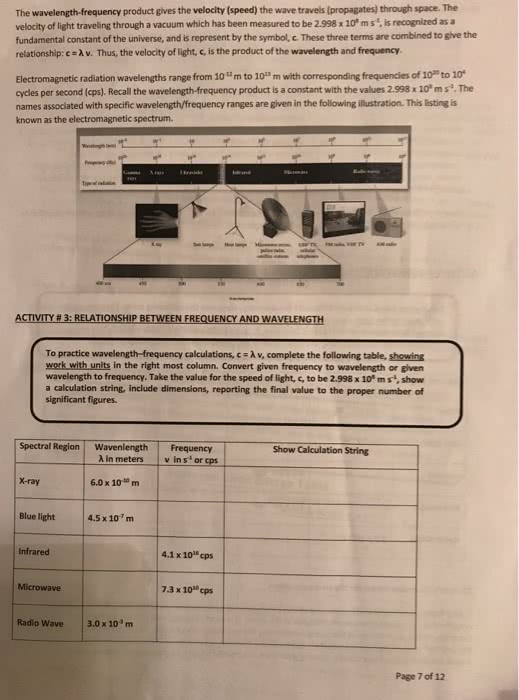
Chapter 2: atomic structure and periodicity: 2. 1: electromagnetic radiation, one of the ways that energy travels through space is by electromagnetic radiation, waves have three primary characteristics, wavelength. Speed of light = 3. 00 x 108 m/s: radiation provides an important means of energy transfer, 2. 2: the nature of matter. Studies in which the frequency of the light is varied show that no electrons are emitted by a given metal below a specific threshold frequency. For light with frequency lower than threshold frequency no electrons are emitted, regardless of the intensity of light. For light with frequency greater than the threshold frequency, the number of electrons emitted increases with the intensity of the light. In bohr"s model the electron is assumed to have a circular path as so is always found at this distance. The principal quantum number is related to the size and energy of the orbital.
