MATH 140 Lecture Notes - Even And Odd Functions, Negative Number, Asteroid Family

• School: McGill University
• Department: Mathematics & Statistics (Sci)
• Course: MATH 140
• Professor: Ewa Duma

Document Summary

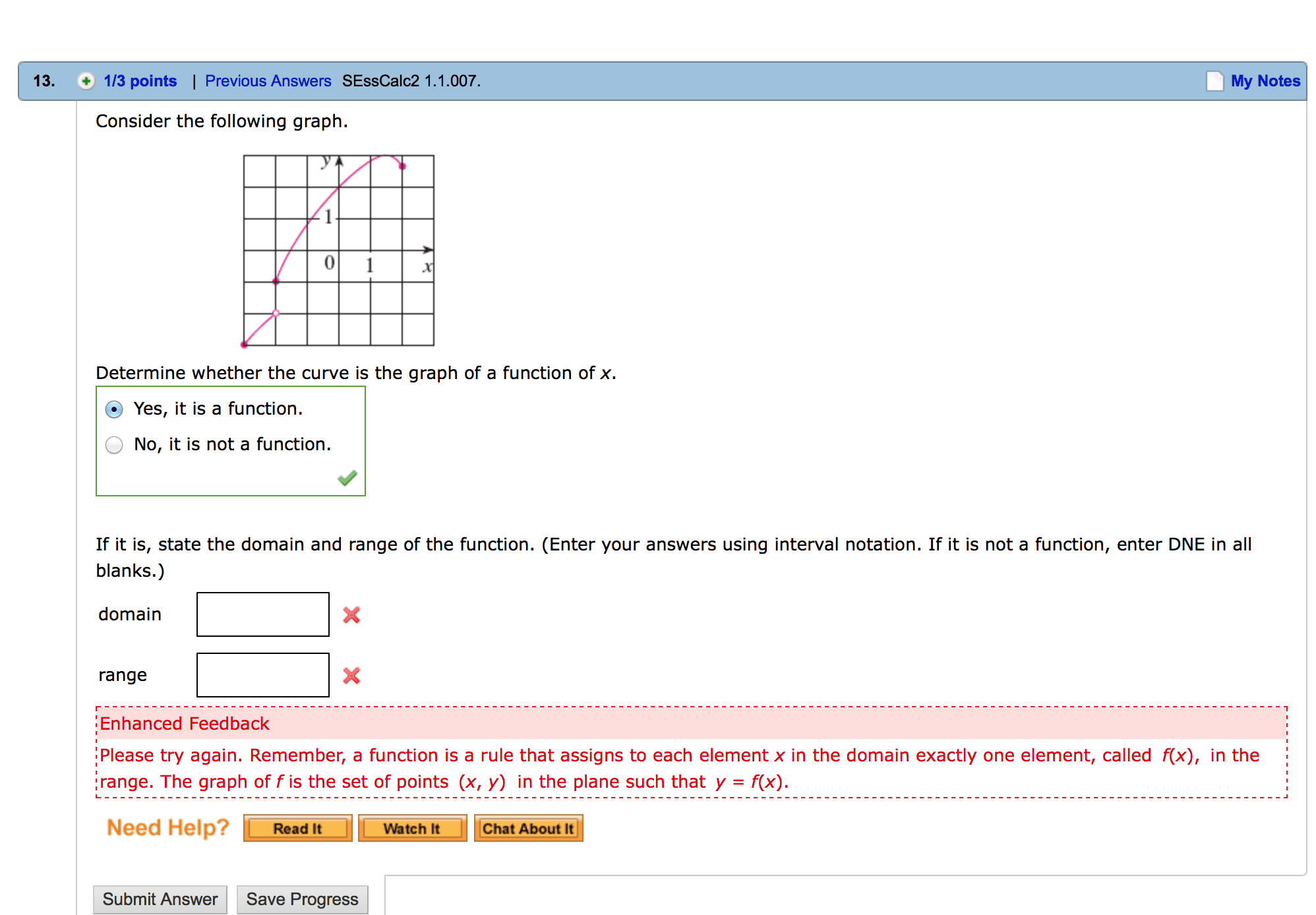
Example 6 find the domain of each function: verbally (description in words, numerically (by a table of values) 1 t x : visually (graph) x 2 x, algebraically (explicit formula) f (b) N if a function is given by a formula and the domain is not stated explicitly, the convention is that the domain is the set of all numbers for which the formula makes sense and de nes a. 1 t is t x x 2 x. 2, t x x x 1 x 2 0 is not allowed, we see that. , so the domain is the interval and division by. Solution (a) because the square root of a negative number is not de ned (as a real number), the domain of consists of all values of x such that. This is equivalent to x 2 (b) since. A rectangular storage container with an open top has a volume of 10 m3.