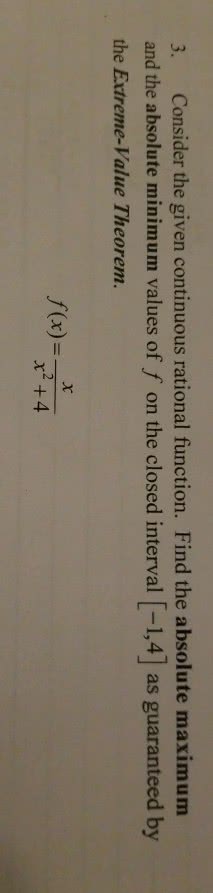MATH 157 Lecture Notes - Jet Fuel, Marginal Revenue, If And Only If

• School: Simon Fraser University
• Department: Mathematics
• Course: MATH 157
• Professor: Chiaka Drake

Document Summary

______________ maximum (y-value): given a function f defined on its domain fd , then f c for all x in f c is the ______________ maximum value. fd , if f x. ______________ minimum (y-value): given a function f c for all x in f defined on its domain f c is the ______________ minimum value. fd , then fd , if f x. ____________ function f defined on some closed interval [ , ]a b will have both an ______________ maximum and an ______________ minimum on the interval. Q1: find the absolute extrema, if they exist, for the following functions defined on the given interval. a) f x. , [ 1,5] b) ( ) 3 g x x. Q2: indicate all absolute and relative extrema on the graph of the function f below for the interval [ 8,6]. Q3: indicate all absolute and relative extrema on the graph of the function f below for the interval [ 1,3].