MATH 157 Lecture Notes - Inverse Function

• School: Simon Fraser University
• Department: Mathematics
• Course: MATH 157
• Professor: Colin Stewart

Document Summary

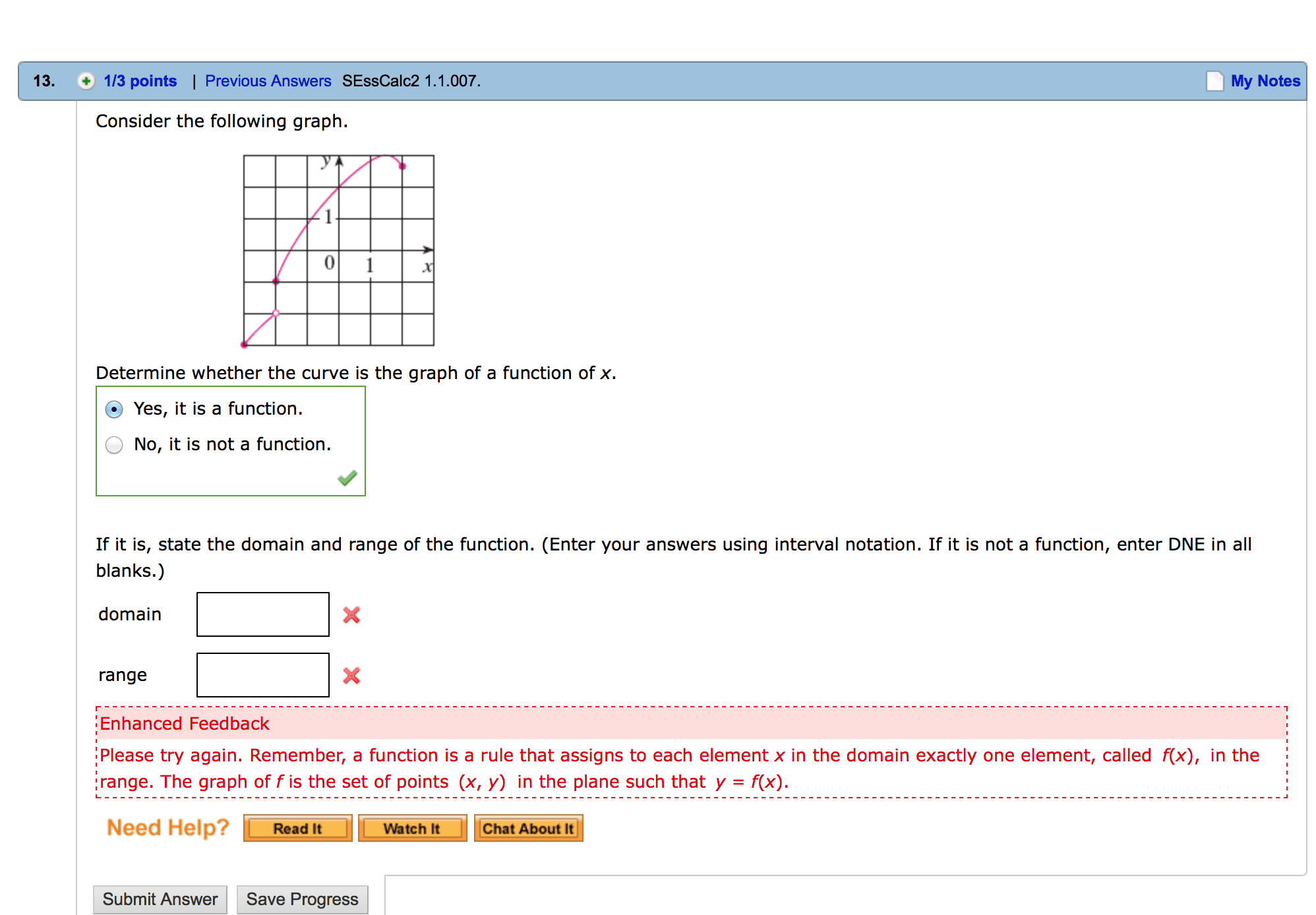
If there are two variables (usually denoted by x and y or s and t) related to each other, then a function is the object to tell us how these two variables related. A function f is a rule that assigns (maps) each element in an set a to one and only one element in an set b. Remarks: every element in a must has a unique image f (x), i. e. x can"t be mapped to more than 1 image (vertical lines test), element in b may not be an image of x in a. Note that f is a function and f (x) is the value of the images of x under f. Let f (x) = x2 + 1 (rule) 1 maps to f (1) = 12 + 1 = 2. 0 maps to f (0) = 01 + 1 = 1 f. Let y = f (x) be a function.