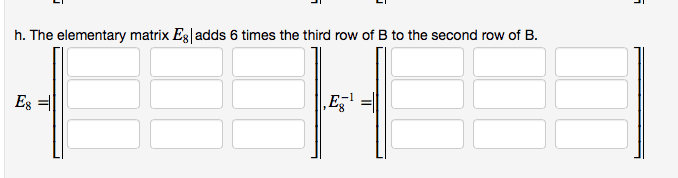MATH125 Lecture Notes - Lecture 20: Elementary Matrix, Invertible Matrix, Identity Matrix

8
MATH125 Full Course Notes
Verified Note
8 documents
Document Summary
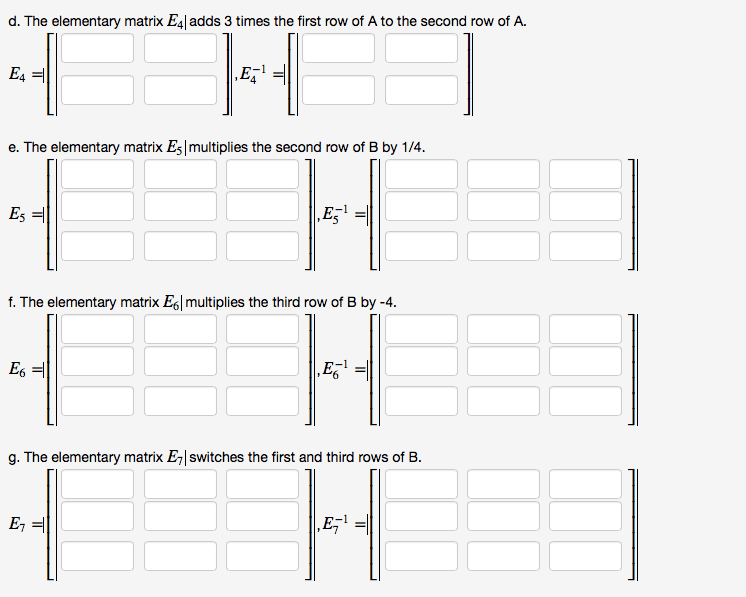
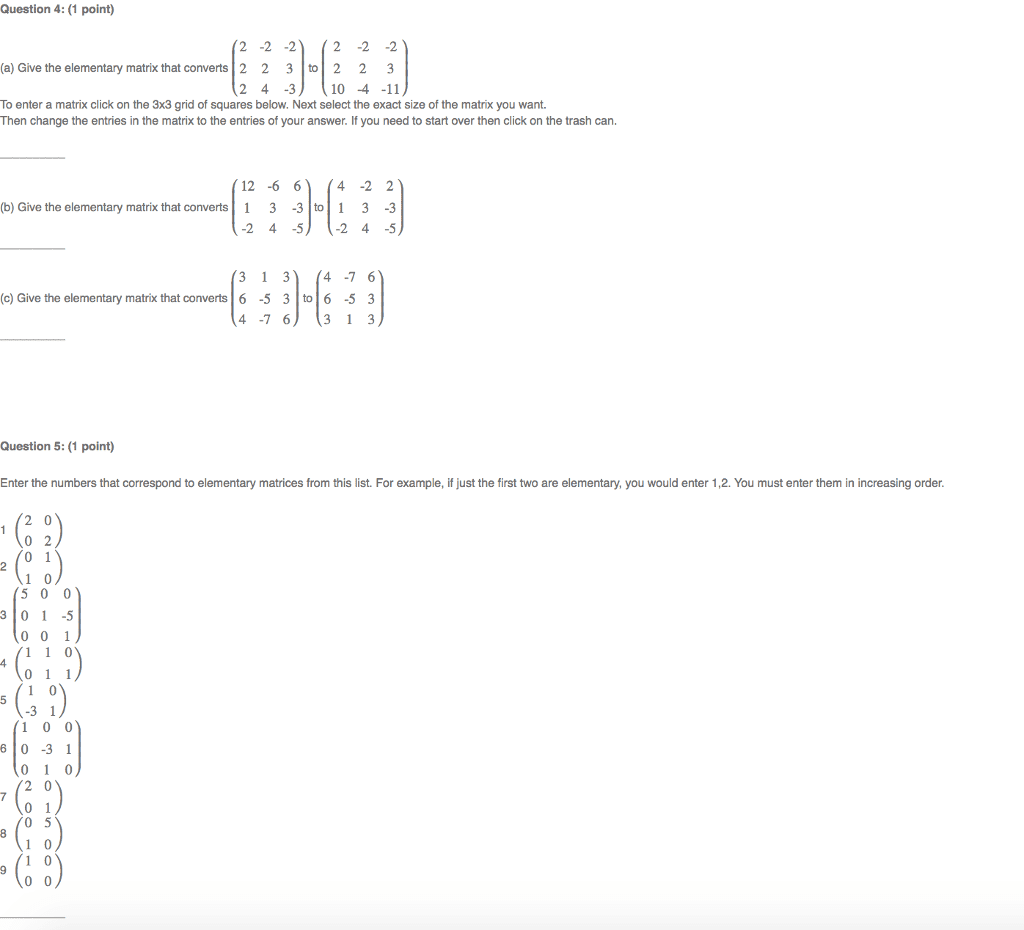
An elementary matrix is one that is obtained by perform- ing a single elementary row operation on an identity matrix. Since there are three types of elementary row operations there are three types of elementary matrices. Indeed if you take the identity matrix i3 and multiply its rst row by 4 and add to row 3 you get e1. Similarly the following two matrices are also elementary: Multiply all entries in row 3 by 5 . Compute e1a, e2a, e3a and describe how these products can be obtained by elementary row operations on a. E1a = a d b e c f g 4a h 4b i 4c. E3a = d e f a b c g h i b e c a d f. In words, the results are: addition of 4 times row 1 to row 3 produces. E1a; an interchange of rows 1 and 2 produces e2a; multiplication of row 3 by 5 produces e3a.