MATH118 Lecture Notes - The Technique, Differentiable Function, Riemann Sum
17 Apr 2013
School
Department
Course
Professor
Document Summary
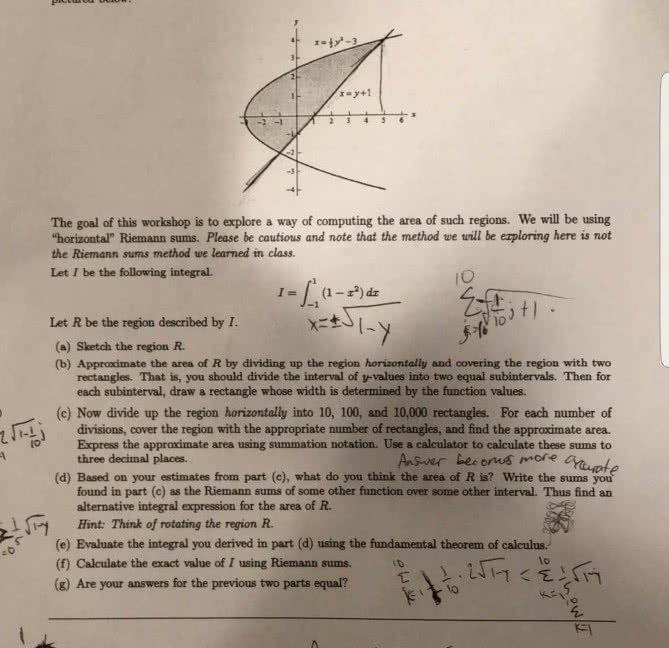
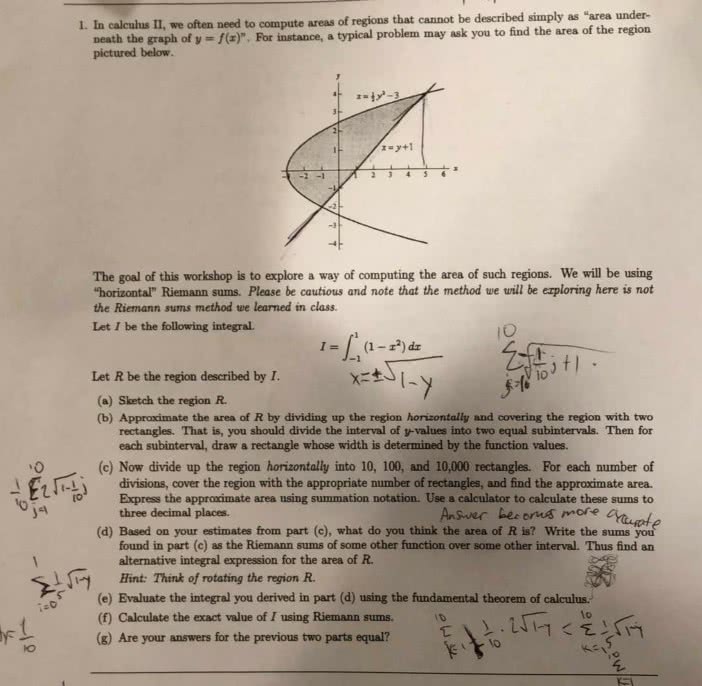
Monday, january 7 lecture 1: integration by substitution (refers to 6. 1 in your text) After having practiced using the concepts of this lecture the student should be able to: define the differential of a function, integrate indefinite integrals by making appropriate change of variables (substitution), integrate definite integrals by appropriate change of variables. Summary of what we have learned about the notion of integration. Our study of integration began with attempts at finding the area of the region bounded by the curve of f(x) and the x-axis over an interval [ a, b]. To do this we introduced the notion of a riemann sum. But computing areas in this way is inefficient. The fundamental theorem of calculus presented an alternate way to compute such numbers. This important theorem is presented into two parts. That is, if f(x) is continuous on [a, b] and f(x) is an anti- derivative of f(x) then.
