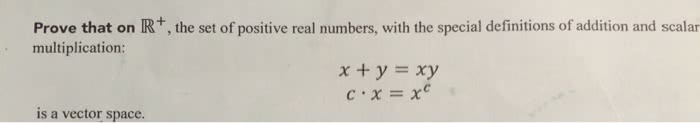MATH136 Lecture Notes - Lecture 19: Scalar Multiplication, Additive Inverse, Subset

Monday, June 12
−
Lecture 19: Abstract vectors spaces (Refers to 4.1)
Concepts:
1. Abstract vector space.
2. Closure under an operation.
3. Prove: If α in ℝ and v in V are such that αv = 0. Then either α = 0 or v = 0.
4. Recognize ℝn, the set of all m by n matrices, Mn,m, and all functions f on [0,1] as
examples of vector spaces.
19.1 Definition − Let V be a set on which we have define addition + and scalar
multiplication. The set (V, +, scalar mult.) is called a vectors space if and only if it
satisfies all of the following axioms:
1) The set V is closed under addition and scalar multiplication.
2) Addition properties:
i. Addition in V is associative and commutative.
ii. There exists in V an element 0 such that v + 0 = v for all v in V. (Additive with 0 axiom)
iii. For all v in V. there exists in V an element
−
v such that v +
−
v = 0. (Additive inverse axiom)
3) Scalar properties:
i. The elements in V distribute over finite sums of scalars.
ii. Scalars distribute over finite sums of elements of V.
iii. (αβ)v = α(βv)
iv. For every v in V, 1v = v. (Scalar mult with 1 axiom)
19.1.1 Remark – In the above definition we use the real numbers as scalars. This is
why we often specify “vector space over the reals”. Denote a vector space along with
its operation + and scalar multiplication as (V, + α).
- The means that we only consider real numbers as scalars. We sometimes speak of
a “vector space over the complex numbers” as a way of saying that we accept
complex numbers as scalars.
19.1.2 Recall − A set is said to be closed under linear combinations mean that for
any two vectors u and v in the set V, αu + βv is also in V.
19.1.3 Definition − A subset W of a vector space V is a subspace of V if and only if it
contains the 0-vector and is closed under linear combinations.
19.1.4 Theorem − Suppose W is a subspace of the vector space (V , +, α).
Then (W , +, α) is itself a vector space. It inherits from V the operations + and scalar
multiplication α which allow it to satisfy all other axioms of a vectors space.
To prove this we need only verify that W satisfies all axioms of a vector space.
(Exercise)
19.2 Proposition : Let (V , +, α) be a vector space. Then:
1. 0v = 0, for all v in V
2. α0 = 0 for all α in ℝ.
3. For all v in V, There is only one vector x such that v + x = 0
4. ( −1)v = −v, for all v in V.
Proof of 1):
- Let w = 0v. Required to show: w = 0.
- Note that w + w = 0v + 0v = (0 + 0)v = 0v = w. So w + w = w. (Scalar axiom invoked)
- Then
0 = w + −w (Addition axiom)
= (w + w) + ( −w) (Addition axiom)
= w + (w + −w) (Associativity of +)
= w + 0 (additive inverse axiom)
= w = 0v (additive identity axiom)
Proof of 2).
- Let α0 = w. Required to show: w = 0.
- Note that w + w = α0 + α0 = α(0 + 0) = α0 = w. So w + w = w. (Scalar axiom invoked)
- Then
0 = w + −w (Addition axiom)
= (w + w) + ( −w) (Addition axiom)
= w + (w + −w) (Associativity of +)
= w + 0 (By previous step and additive identity axiom)
= w = α0 (Addition with additive inverse axiom)
Proof of 3) (showing that for all v in V, −v is unique) is left as an exercise (done in class).

34
MATH136 Full Course Notes
Verified Note
34 documents
Document Summary
Monday, june 12 lecture 19: abstract vectors spaces (refers to 4. 1) Concepts: abstract vector space, closure under an operation, prove: if in and v in v are such that v = 0. Then either = 0 or v = 0: recognize n, the set of all m by n matrices, mn,m, and all functions f on [0,1] as examples of vector spaces. 19. 1 definition let v be a set on which we have define addition + and scalar multiplication. There exists in v an element 0 such that v + 0 = v for all v in v. (additive with 0 axiom) For all v in v. there exists in v an element v such that v + v = 0. (additive inverse axiom: scalar properties, the elements in v distribute over finite sums of scalars. Scalars distribute over finite sums of elements of v. ( )v = ( v)