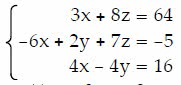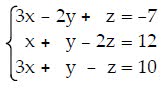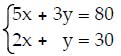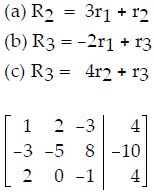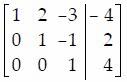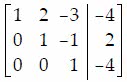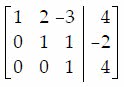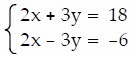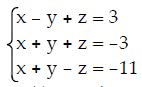Q20. Find functions f and g so that f â g = H(x) = (5 - 2x3)2.
a. f(x) = 5 - 2x3 ; g(x) = x2
b. f(x) = (5 - 2x)3 ; g(x) = x2
c. f(x) = x2 ; g(x) = 5 - 2x3
d. f(x) = x3 ; g(x) = (5 - 2x)2
Q29. Solve the system of equations using Cramer's Rule if it is applicable.
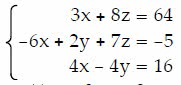
a. x = 9, y = 2, z = 5; (9, 2, 5)
b. x = 8, y = 4, z = 5; (8, 4, 5)
c. x = 4, y = 5, z = 4; (4, 5, 4)
d. x = 8, y = -4, z = -5; (8, -4, -5)
Q30. Solve the system of equations using matrices (row operations). If the system has no solution, say that it is inconsistent.
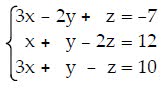
a. x = 2, y = 3, z = -7; (2, 3, -7)
b. x = 1, y = 3, z = -4; (1, 3, -4)
c. x = 5, y = 13/2, z = -3; (5, 13/2, -3)
d. x = 1, y = -3, z = -16; (1, -3, -16)
Q33. Write the partial fraction decomposition of the rational expression (4x3 + 4x2)/(x2 + 5)2.
a. (4x - 4)/(x2 + 5) + (-20x + 20)/(x2 + 5)2
b. (4x + 4)/(x2 + 5) + (-20x - 20)/(x2 + 5)2
c. (4x + 4)/(x2 + 5) + (20x - 20)/(x2 + 5)2
d. (4x + 4)/(x2 + 5) + (20x + 20)/(x2 + 5)2
Q34. Solve the linear programming problem. Minimize z = 11x + 6y + 7 subject to: x = 0, y = 0, x + y = 1.
a. minimum: 7
b. minimum: 18
c. minimum: 24
d. minimum: 13
Q35. Solve the system of equations by elimination.
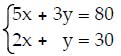
a. x = 10, y = 0; (10, 0)
b. x = 10, y = 10; (10, 10)
c. x = 0, y = 10; (0, 10)
d. x = 0, y = 0; (0, 0)
Q36. Perform the row operations on the given augmented matrix.
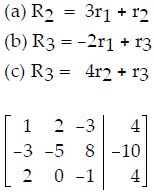
a. 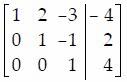
b. 
c. 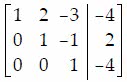
d. 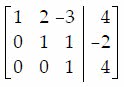
Q37. Solve the system of equations using Cramer's Rule if it is applicable.
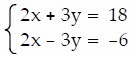
a. x = -4, y = 3; (-4, 3)
b. x = -3, y = -4; (-3, -4)
c. x = 4, y = 3; (4, 3)
d. x = 3, y = 4; (3, 4)
Q38. Write the partial fraction decomposition of the rational expression x/(x2 - 9x + 20).
a. -4/(x - 4) + 5/(x - 5)
b. -5/(x - 4) + 4/(x - 5)
c. 4/(x - 4) + -5/(x - 5)
d. -4/(x - 4) + -5/(x - 5)
Q39. Solve the system of equations.
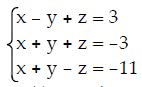
a. x = -4, y = 4, z = -3; (-4, 4, -3)
b. x = -3, y = 4, z = -4; (-3, 4, -4)
c. x = -4, y = -3, z = 4; (-4, -3, 4)
d. inconsistent
Q40. Find the value of the determinant.

a. 224
b. 24
c. -72
d. 72
3x + 8-64 -6x + 2y + 7z =-5 4x-4y = 16 456 874
Show transcribed image text 3x + 8-64 -6x + 2y + 7z =-5 4x-4y = 16 456 874