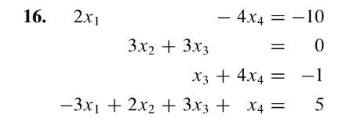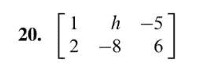MATA23H3 Lecture : Linear system, REF, RREF, nullspace
Document Summary
Definition: an m n linear system of equations is a system of m linear equations in n variables: a11x1 + a12x2 + + a1nxn. Definition: an m n matrix is an ordered rectangular array, of real numbers, with m rows and n columns. a11 a12 a21 a22 am1 am2. Amn: we may denote the matrix by giving it a name, say a, and write. A matrix with zero entries only is called, a zero matrix and is denoted by o. Find a + b and 2a 3b. www. notesolution. com. Definition: let a be an n m matrix and b be an m k matrix. Then ab is de ned to be the n k matrix with the ijth entry given by (ab)ij = (ith row of a) (jth column of b). Letting ai be the ith row of a and bj be the jth column of b, then. 0 1 (cid:12)(cid:12)(cid:12) (cid:12)(cid:12)(cid:12) b1 b2 (cid:12)(cid:12)(cid:12) (cid:12)(cid:12)(cid:12)