CHM135H1 Lecture Notes - Exponential Decay, Rate Equation, Reaction Rate

90
CHM135H1 Full Course Notes
Verified Note
90 documents
Document Summary
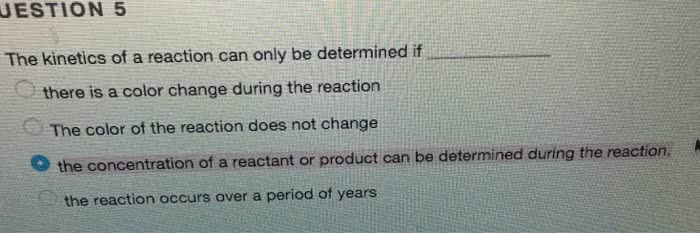
Reaction rate is determined by [reactant/product]/ time. [] with time can be determined by the pressure as gas molecules are produced. The general rate of reaction is the rate of one reactant or product, divided by the coefficients of the other reactants/products: eg) for 2n2o5(g) 4no2(g) + o2(g), *o2+/ t = -(1/2)( *n2o5]/ t) = (1/4)( *no2]/ t+ Depend on [reactions] and decreases as reactants are used up. Instantaneous rate is over a specific time t rather than an interval. Rate law represents the dependence of rate on []. If m or n is one, the rate depends linearly on [reactant]. Eg) if m=1 and [a] doubles, then the rate doubles as well. Eg) if m=2 and [a] doubles, then the [a] is quadrupled and the rate increases by a factor of 4: rate is proportional to [a]m or [b]n. M and n give the respective reaction orders.