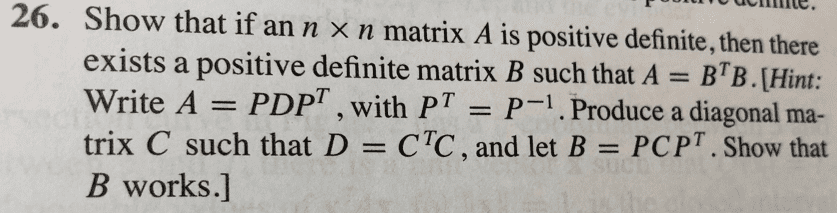MAT224H1 Lecture : Lengths and distrances (inner products), angles, cauchy-schwartz inequality, triangle inequality
Document Summary
Exercise: prove that the determinant of a positive-de nite matrix is a pos- itive number. Solution 1(due to kirby): let a be a positive-de nite matrix. Since it is hermitian (and every complex positive de nite matrix by de nition is. Hence det a is the product of a"s eigenval- ues. Since the eigenvalues of a positive-de nite matrix are real and positive, their product is also positive. Solution 2(due to kristie): since a is positive-de nite, there exists an invertible matrix b such that a = b b. 2 lengths and distances in inner product spaces. If v is an inner product space we can de ne the length of a vector by the formula kvk = p(v, v) This length is also called the norm of the vector v and we use the symbol kvk instead of |v| to distinguish it from the length computed using the standard dot-product on rn.