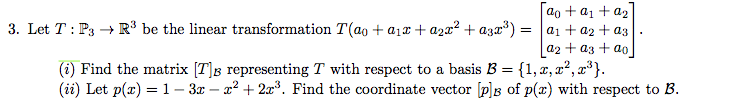MAT224H1 Lecture : Using coordinates, Algebra Transformations, Change of Basis, change of basis for transformation
Document Summary
We are going to expand on the idea that while one should think about vectors in vector spaces and linear transformations, computations should be done with coordinates and transformation matrices1. Example: let t : p2 p1 be the di erentiation mapping t (p) = p . Let a = (1 x, 1 + x, 1 + x + x2), b = (1 x, x) be bases of p2 and p1 respectively. Find [t ]b,a and use it to nd a basis for ker t and imt . Solution: to nd [t ]b,a we should apply t to basis vectors from a and express the results as linear combinations of vectors from b. For the vector 1 x we have [t (1 x)]b = [ 1]b. To nd [ 1]b we should express 1 as 1 (1 x) + 2 x for some.