STA437H1 Lecture Notes - Royal Institute Of Technology, False Discovery Rate, Principal Component Analysis
Document Summary
Notes for sta 437/1005 methods for multivariate data. Let x be a random vector with p elements, so that x = [x1, . , xp] , where denotes transpose. (by convention, our vectors are column vectors unless otherwise indicated. ) We denote a particular realized value of x by x. The expectation (expected value, mean) of a random vector x is e(x) = r xf (x)dx, where f (x) is the joint probability density function for the distribution of x. We often denote e(x) by , with j = e(xj) being the expectation of the j"th element of x. The variance of the random variable xj is var(xj) = e[(xj e(xj))2], which we some- times write as 2 j . The standard deviation of xj is pvar(xj) = j. The covariance of xj and xk is cov(xj, xk) = e[(xj e(xj))(xk e(xk))], which we sometimes write as jk.




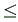 y1
y1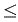 1 , 0
1 , 0 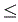 y2
y2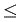 1
1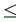 1/2, Y2
1/2, Y2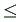 3/4).
3/4).

