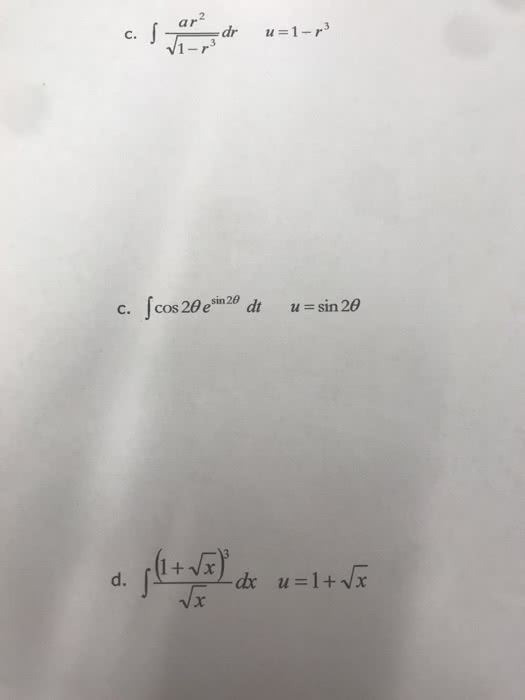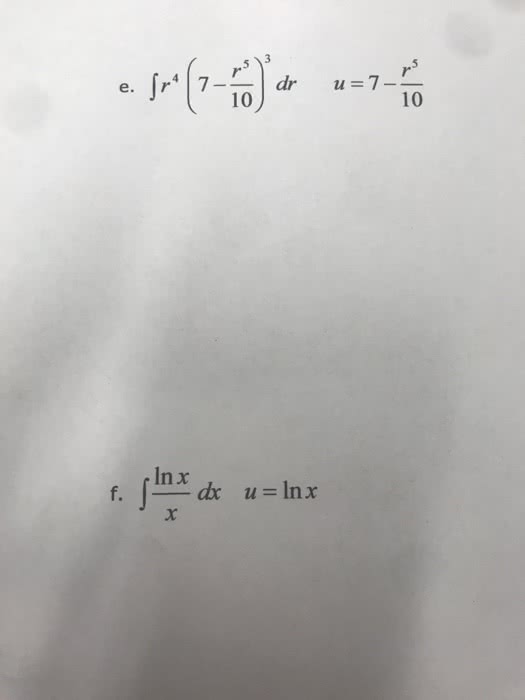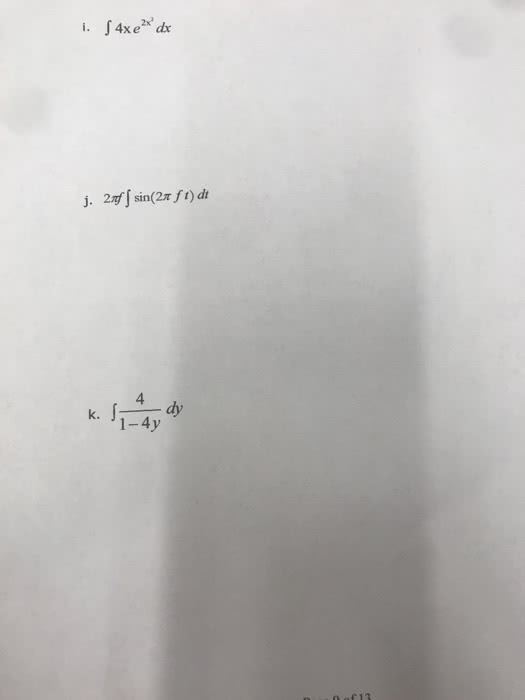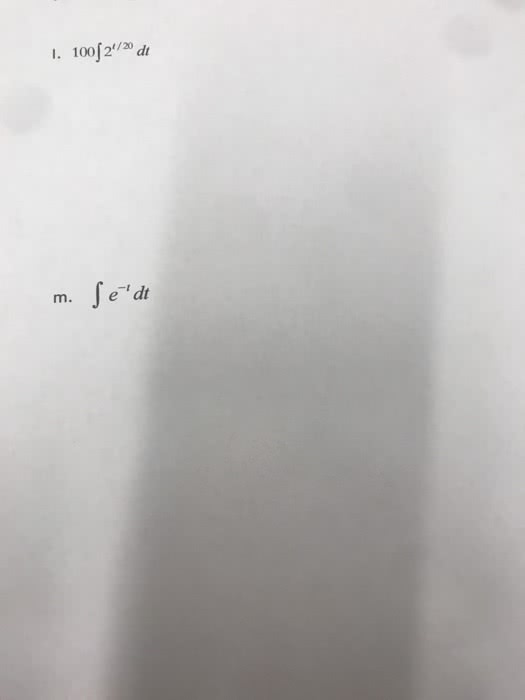MATH 2B Lecture 6: Substitution Rule
MATH 2B verified notes
6/30View all
Document Summary
Math 2b - lecture 6 - substitution rule. We introduce a new variable u=2x, then the integral becomes: s in(2x) dx u=2x s in u dx. Since dx is not consistent with our new variable u, we then need to translate dx to du. dx = du du = 2dx u=2x s in(2x) dx u=2x s inu dx dx= du s inu du. After introduction the new variable u, and some translations, we end with the integral. This example illustrates the basic idea of u-substitution. If u=g(x) is a differentiable function whose range is an interval i and f is continuous on i, then: f (g(x))g (x)dx u=g(x) f (u) du u = g(x) du = g"(x)dx. That means, if we recognize there is a composite function ( f(g(x)) ), it is possible to use the u-sub to simplify the function, such that we can solve the integral much easier.