MATH 222 Study Guide - Quadric, Tangent Space, Level Set
Document Summary
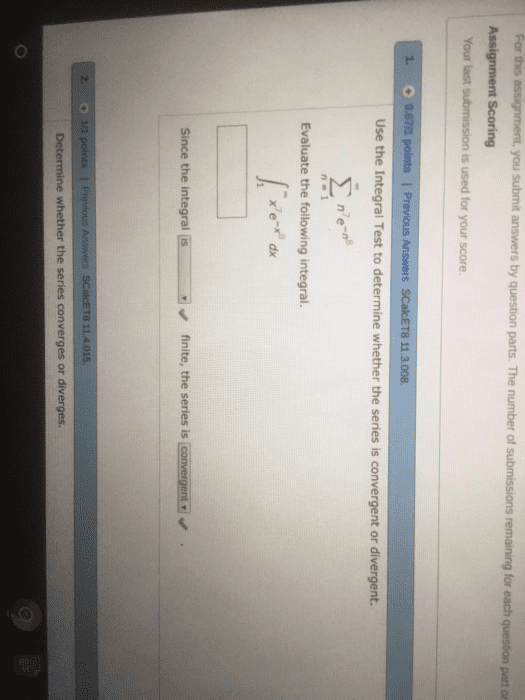
Page 1 of 4: approximate the given de nite integral correct to 5 decimal places (i. e. , within 0. 5 10 5): 0: a function f (x) has maclaurin series: Nd f (k)(0) for all positive integer k: (a) use the binomial series to nd the maclaurin series for f (x) = arcsin x and its radius of convergence (hint: arcsin x = r x. Page 2 of 4: find the equations of the tangent plane and normal line of the surface x2 + y2 + z = 6 at the point. P (2, 1, 1): if z = f (x, y) is implicitly de ned by x2z + sin(yz) = y sec z, nd z. Assume that second order partial derivatives of f are continuous. circle x2 + y2 = 1: let z = f (x, y) be a surface and f (x, y) = c a level curve on that surface.