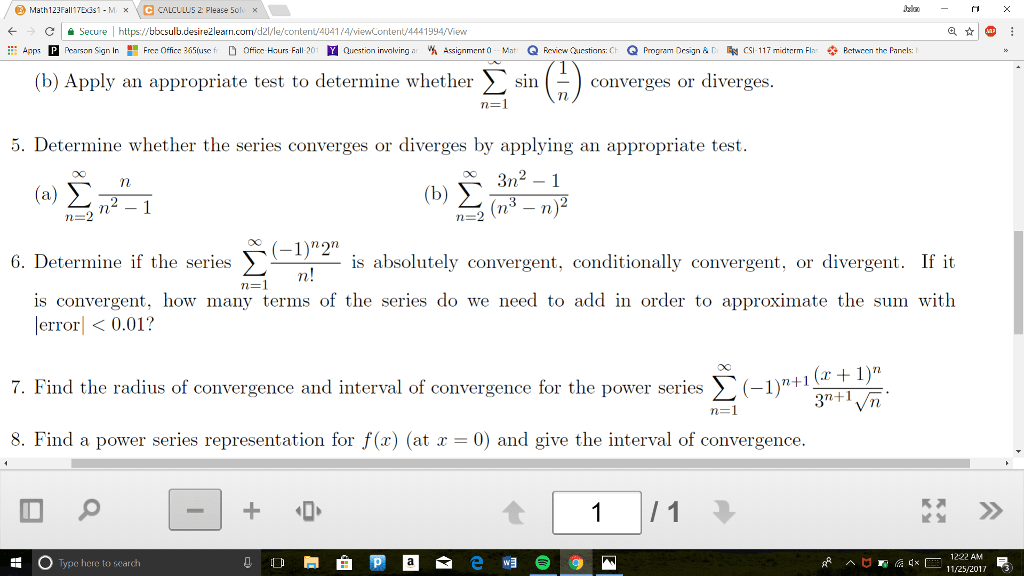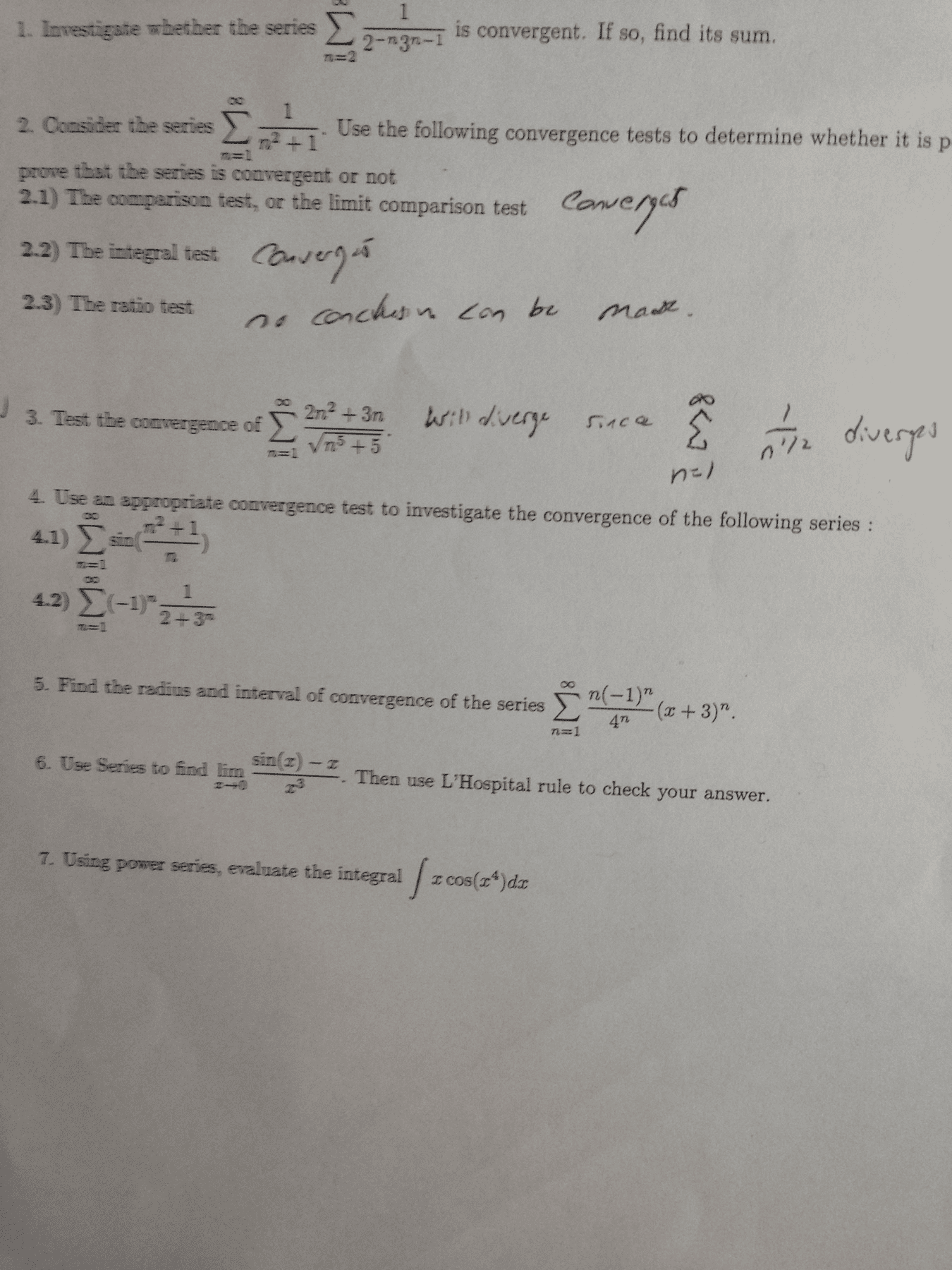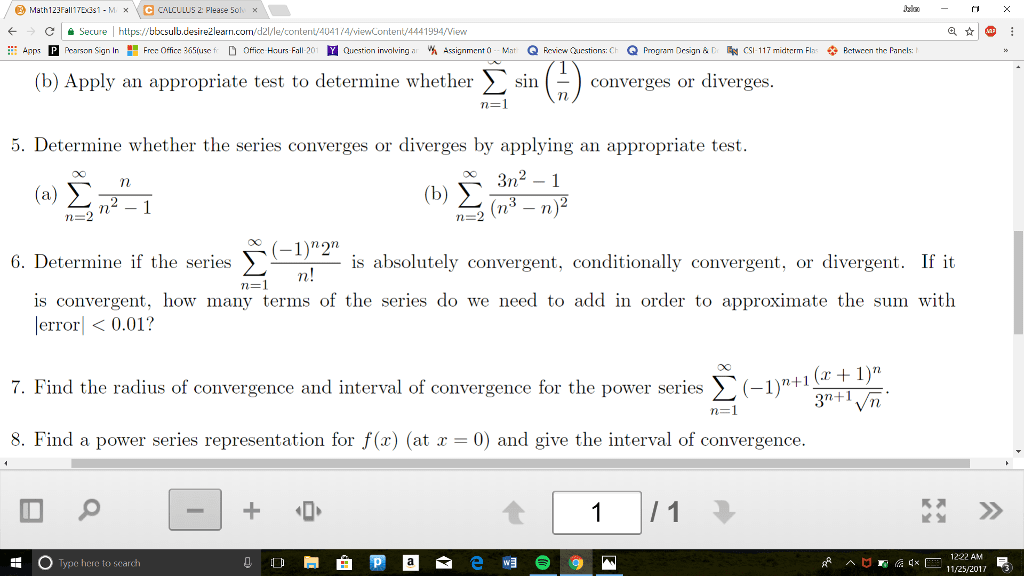MATH214 Study Guide - Quiz Guide: Alternating Series Test, Ratio Test, Alternating Series

• School: University of Alberta
• Department: Mathematics
• Course: MATH214
• Professor: Pierre Youssef

Document Summary

Instructions: show your work, answers should be explained. Do not speak to or communicate with other students. Find the radius and interval of convergence of the following series: 22n ln2(n) ( 3)n n (x 3/4)n. Answer is not written problem is not solved! The general term is an = ( 1)n ln2(n) ing series test, we need to check that ln2(n) Now if we calculate the derivative of f (x) = ln2(x) whenever x (cid:62) e2. Therefore for n (cid:62) 9, ln2(n) n n that(cid:80) which is negative is decreasing. By the alternating series test, we deduce n(cid:62)9 an is convergent. Since the rst 8 terms won"t a ect the convergence we deduce that the n x we get f(cid:48)(x) = ln(x) (2 ln(x)) x2 is decreasing and goes to zero. Now to check if the series is absolutely convergent, we need to consider the series of the absolute values.