MAT135H1 Study Guide - Final Guide: Function Composition

144
MAT135H1 Full Course Notes
Verified Note
144 documents
Document Summary
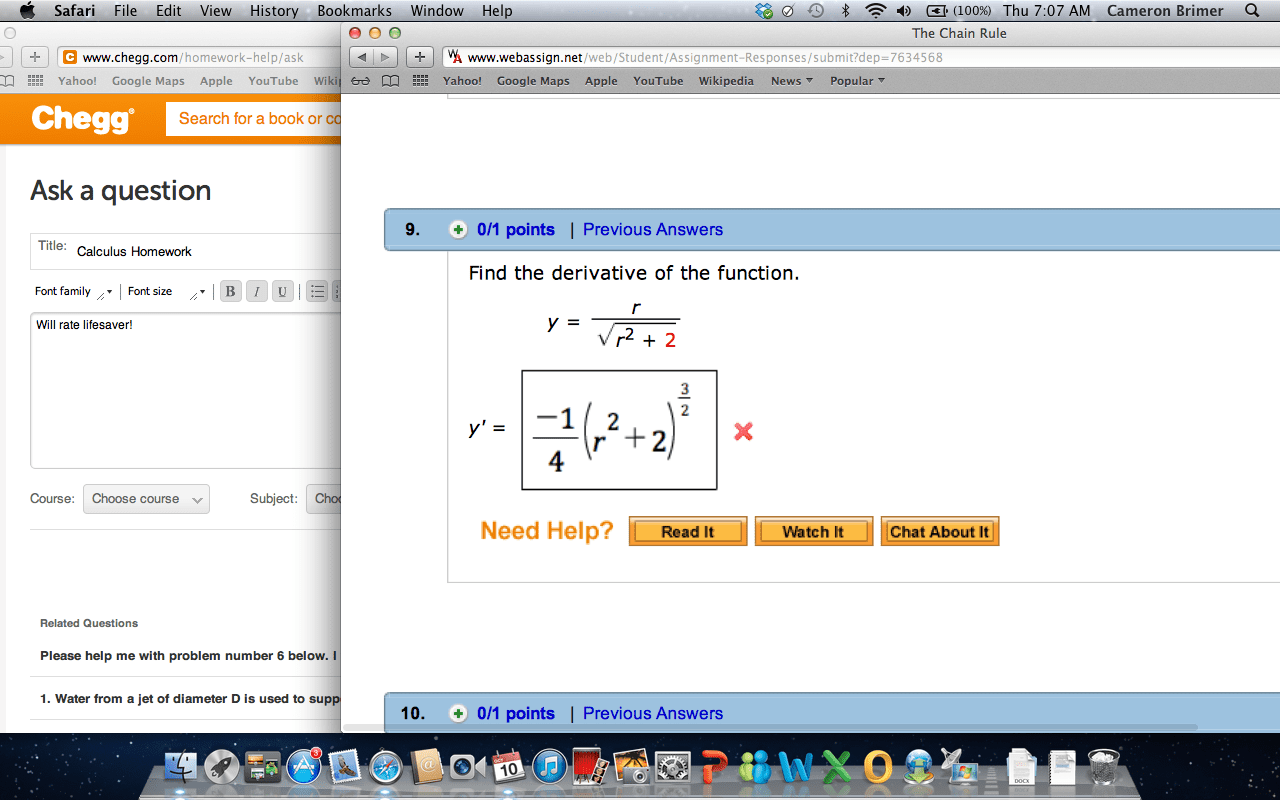
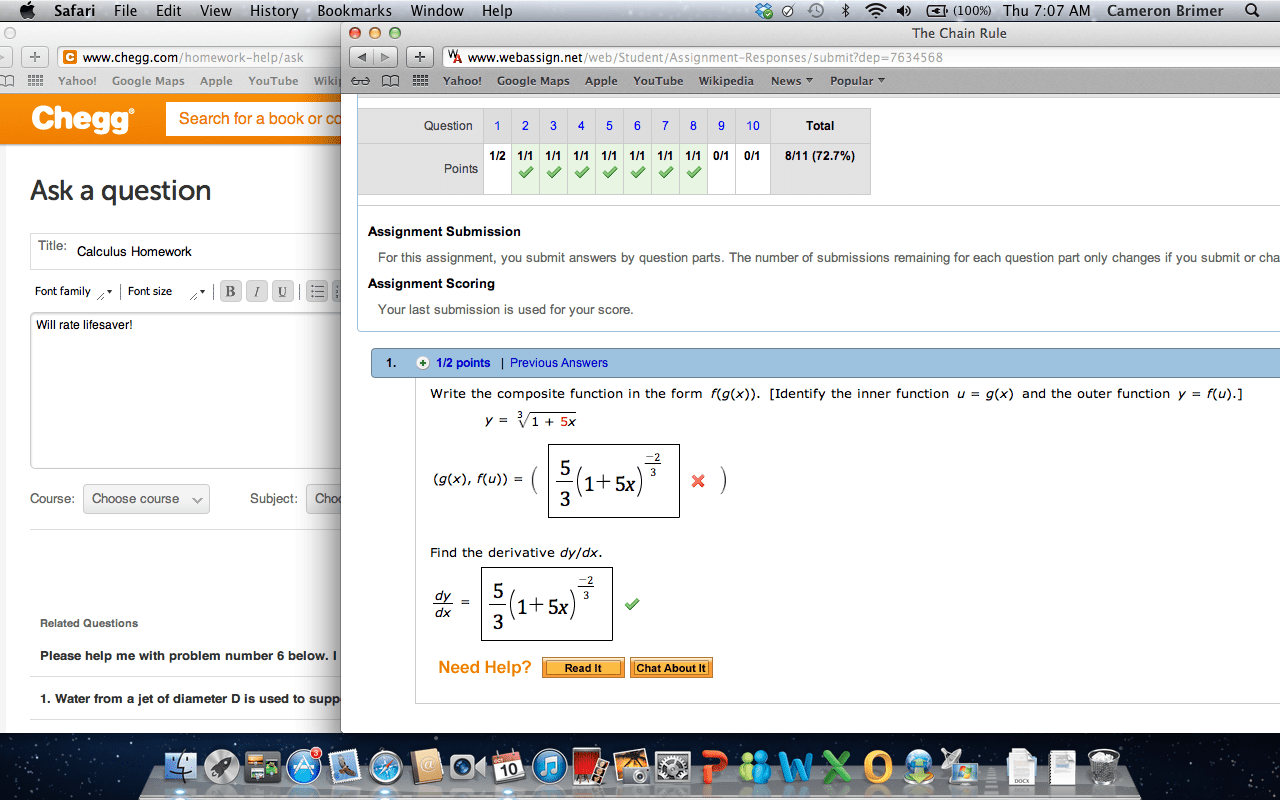
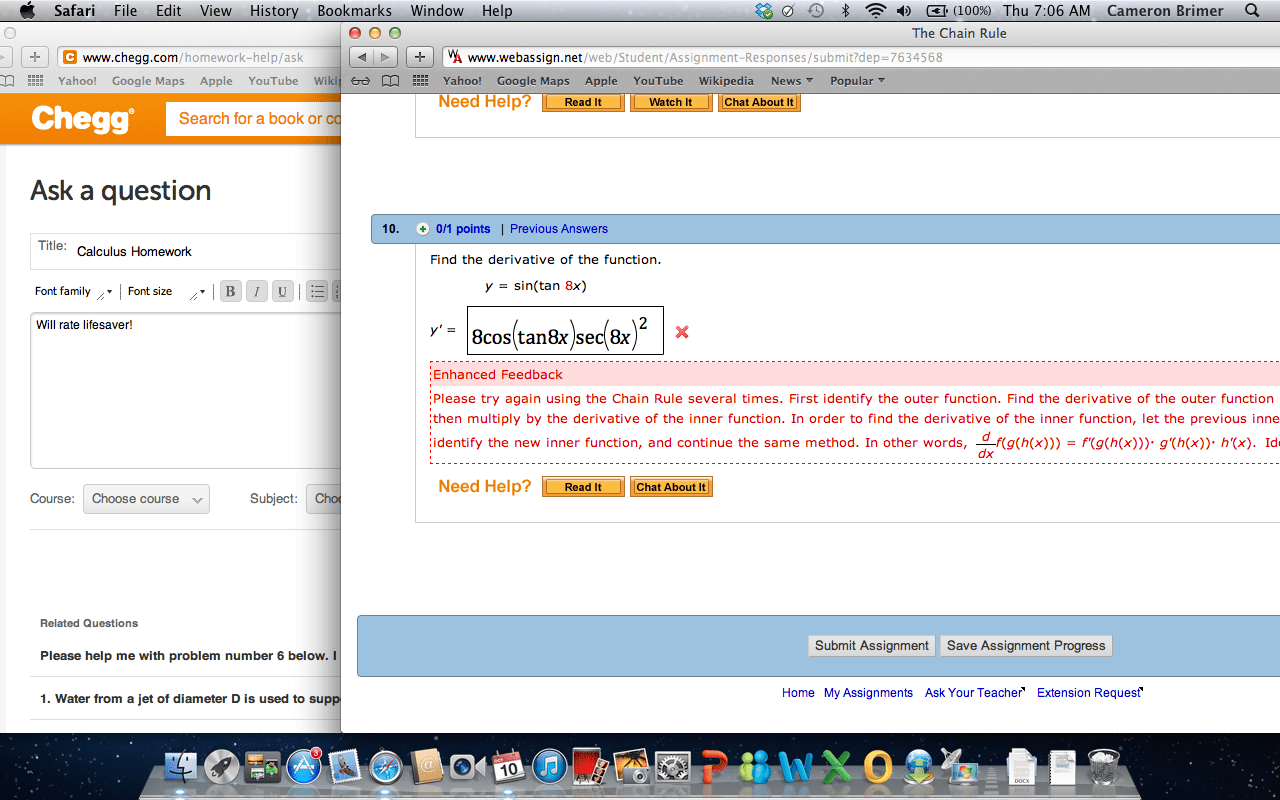
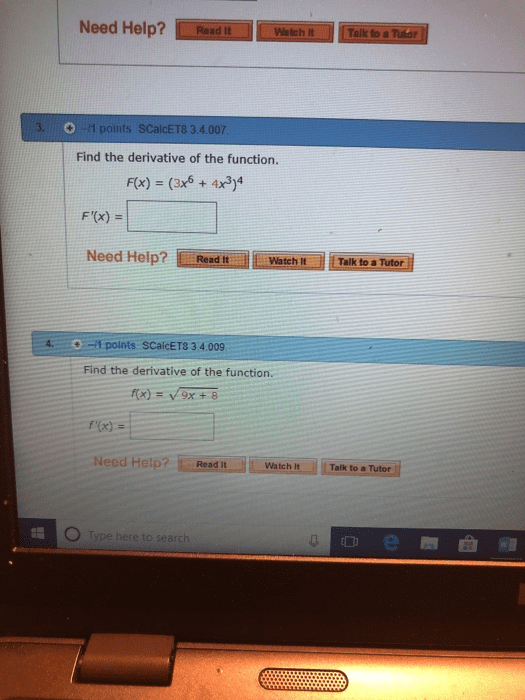
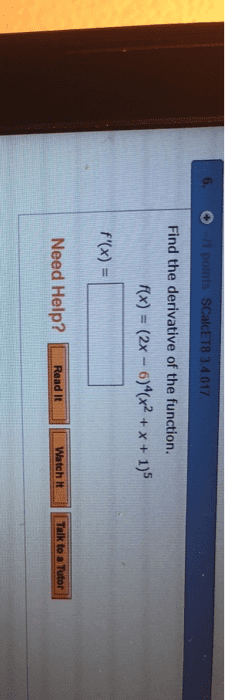
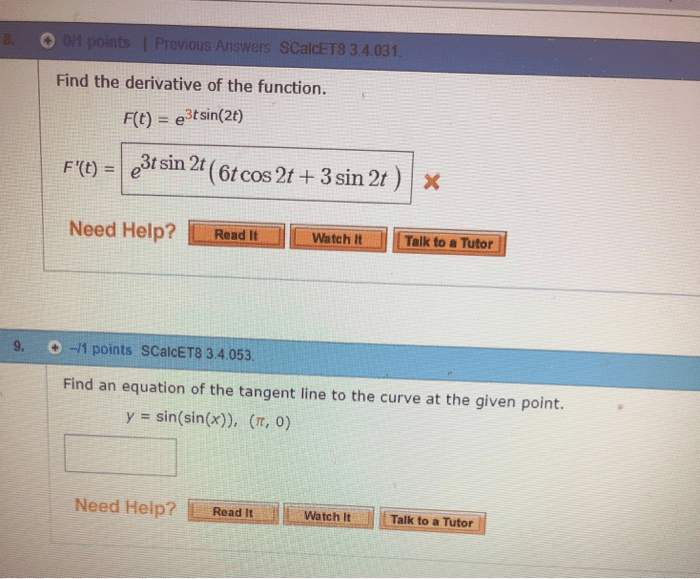
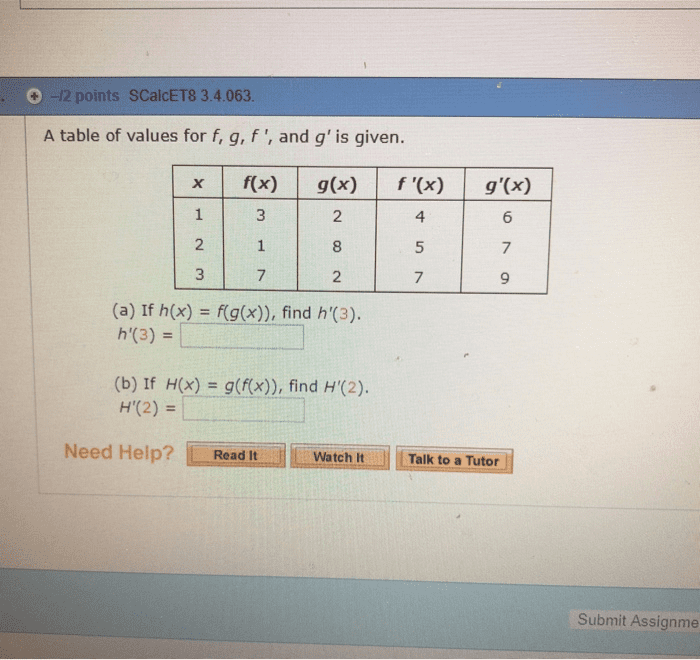
Composite function: given two functions f x and ( )g x , a composite function is defined as: f glad of gcfcx. Example 1: given f x x= and g x x= + , determine. If f" and g" are functions, then the derivative of the composite function h x f g x is h x. Leibniz notation: if y" is a function of u" and if u" is a function of x" then ddxt ddf. dz: note: the power of a function rule (section 2. 3) is a special case of the chain rule: 4 x = d at xu 4y didnt d. 2 hi f 9cd9 x 2 t x t. Express your answer in simplified factored form. h x. 4 x 5 t x2 351 3 4 5774. 4 x x 2 t 3 3 4x 5 3 t l 2 x 2 t 3 4 4x d2 t 3 3 4 5 2 2.