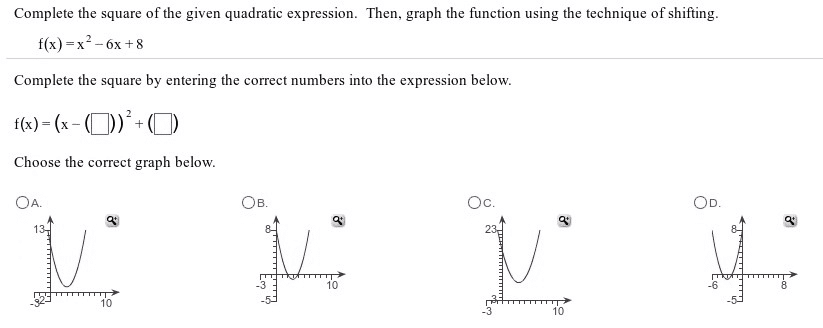
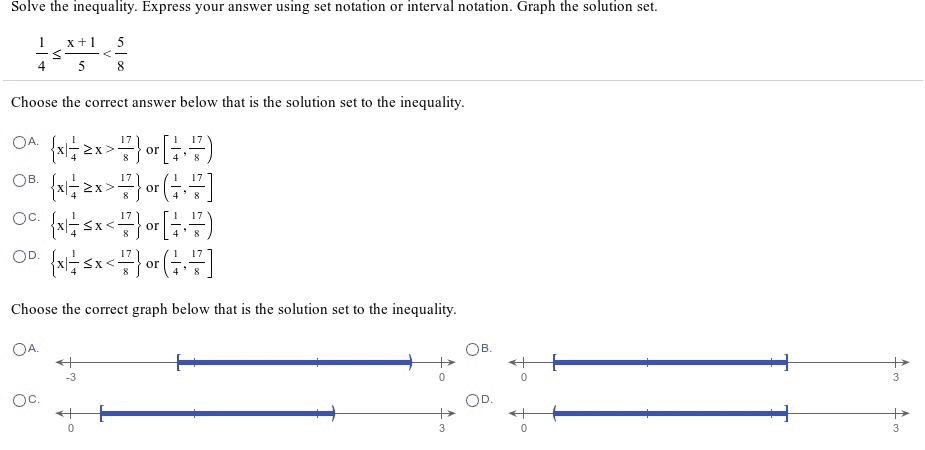
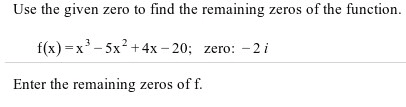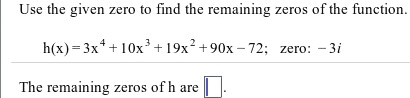1. One of the tables below contains (x,y) values that weregenerated by a linear function. Determine which table, and thenwrite the equation of the linear function represented by the
Table #1 x 2 5 8 11 14 17 20 y 1 3 7 13 21 31 43
Table #2 x 1 2 3 4 5 6 7 y 10 13 18 21 26 29 34
Table #3 x 2 4 6 8 10 12 14 y 1 6 11 16 21 26 31
2. Give an example of each of the following:
A function whosedomain is [2, infinity)
A system of equationswith no solutions
3. For f(x) =1/x^2-3, find:
4. For f(x) = 1/x-5and g(x) = x^2+2, find:
1. (fog)(x)
2. (gof)(6)
5. For the sequencegiven by a (subscript n) = 4n+5 an=4n+5, answer the following:
Find the sum of thefirst 25 terms.
Is this an arithmeticsequence? If so, how can you tell? If not, why not?
6. Graph the areabound by y<1/2x+6, x+3y>=12, x>=0, and x<=12
7. For the functiondefined by:
f(x)= {x^2,x<=1}
{2x+1,x>1}
a. evaluate f(0)
b. graph f(x)
8. Solve thefollowing system of equations algebraically. Verify your solutioneither graphically or by using matrices.
3x-y=0
5x+2y=22
9. Solve thefollowing system of equations algebraically. Verify your solutioneither graphically or by using matrices
8x-2y=5
-12x+3y=7
10.Given matricesA, B, and C below, perform the indicatedoperations if possible. If the operation is not possible, explainwhy.
A (3x3) [1st 2, -1,0] [2nd 0, 5, 0.3] [3rd 1, 4, 10]
B (3x3) [1st 5, 0, 2][2nd 1, -3, 9] [3rd2, 0, 4]
C (1x1) [1, 3, 5]
1.3A+B
2. B+C
3. CA
11. Given the tablebelow, evaluate the following:
x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
f(x) | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
g(x) | -1 | -2 | -3 | -4 | -5 | -6 | -7 | -8 | -9 |
a.(3f+2g(1) b. (fog)(-1)
12.Express the following function, F(x) as a composition of twofunctions f and g
f(x)= x^2/(x^2+4)
13.You have a coupon for your favorite clothing store for $25 off anypurchase of more than $50. The store is also running a 20%-off saleon its entire inventory. Let x be the original price, f(x)be the price with the $25 coupon applied, and g(x) be the pricewith the 20% discount applied.
a.Write an expression for f(x)
b.Write an expression for g(x)
c.What would the expression (fog)(x) represent?
d.What would the expression (gof)(x) represent?
e.If the store allows you to apply both the 20% discount and the$25-off coupon, does it matter which you apply first? How do youknow?