MAT224H1 Final: Examples of change of basis, invertable functions, invertable transformations
Document Summary
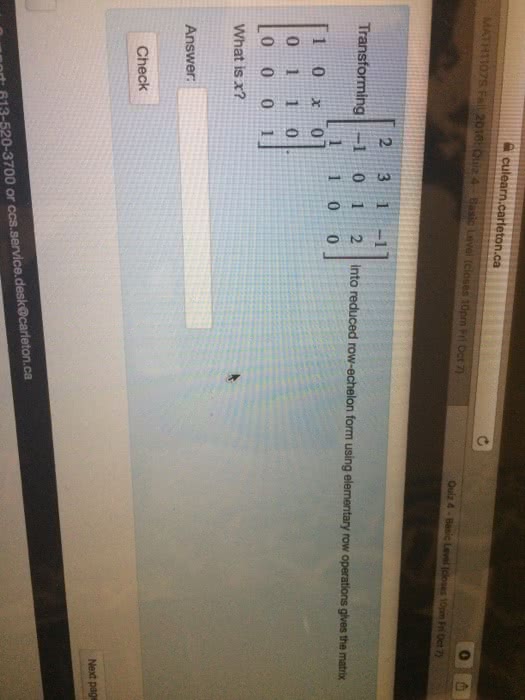
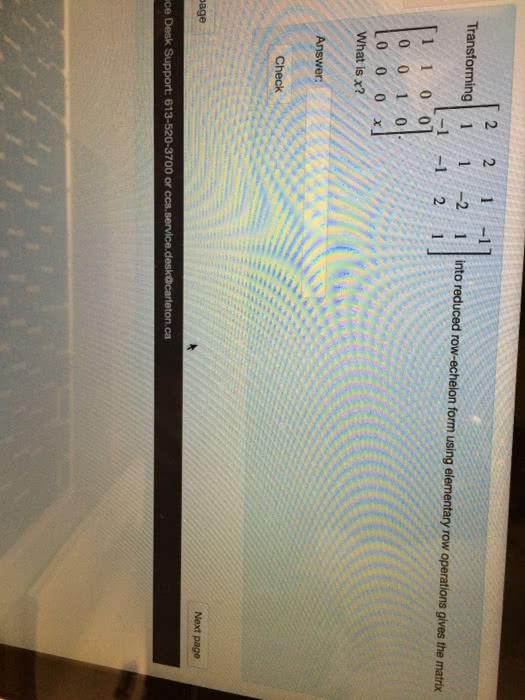
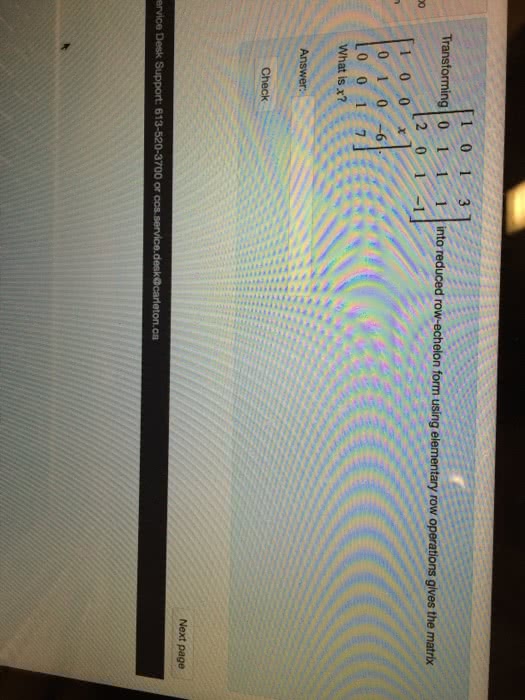
In particular changing the basis in the domain of t results in performing column-operations to its transformation matrix. Similarly, changing the basis in the range of t results in performing row-operations to its transformation matrix. Example: find bases a , b of p2 and p1 so that the transformation is in its reduced row-echelon form, where t : p2 p1, matrix [t ]b . T (a + bx + cx2) = (a 3b + c) + (2a 6b + 3c)x. The idea is to start with arbitrary bases a, b of p2 and p1. With respect to these bases the matrix of the transformation t is likely not to be in its row-reduced form. We can row-reduce it and nd a matrix p so that p [t ]b,a is the row-reduced form of [t ]b,a. We can then try to nd a basis b such that [i]b . ,b [t ]b,a is in the reduced row-echelon form.