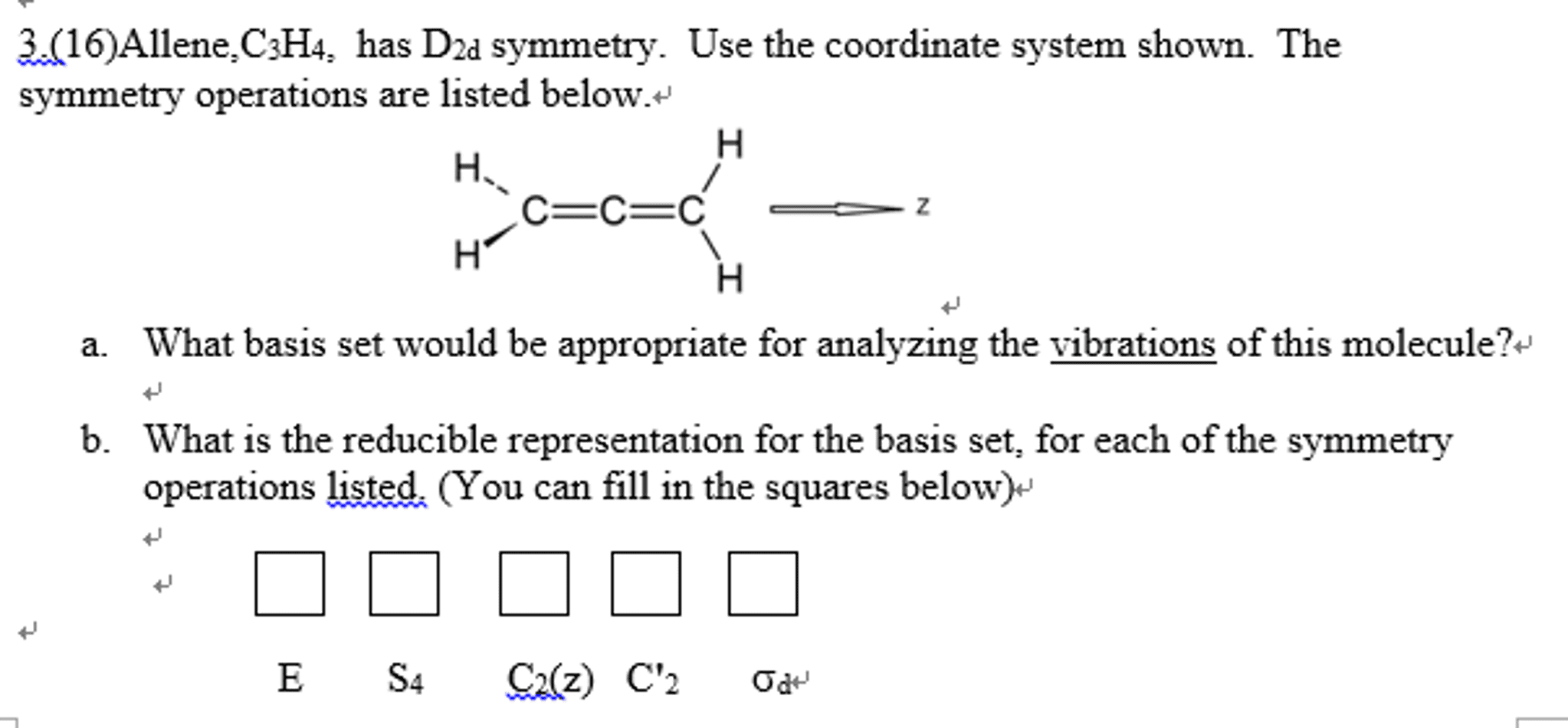
CHEM 212 Lecture Notes - Symmetry Operation, Indo, Ammonia
Document Summary
Symmetry is a phenomenon of the natural world, as well as the world of human inven- tion (figure 4-1). In nature, many types of flowers and plants, snowflakes, insects, cer- tain fruits and vegetables, and a wide variety of microscopic plants and animals exhibit characteristic symmetry. Many engineering achievements have a degree of symmetry that contributes to their esthetic appeal. Examples include cloverleaf intersections, the pyramids of ancient egypt, and the eiffel tower. Symmetry concepts can be extremely useful in chemistry. By analyzing the sym- metry of molecules, we can predict infrared spectra, describe the types of orbitals used in bonding, predict optical activity, interpret electronic spectra, and study a number of additional molecular properties. In this chapter, we first define symmetry very specifi- cally in terms of five fundamental symmetry operations. We then describe how mole- cules can be classified on the basis of the types of symmetry they possess.