Can you please help me with number 5?
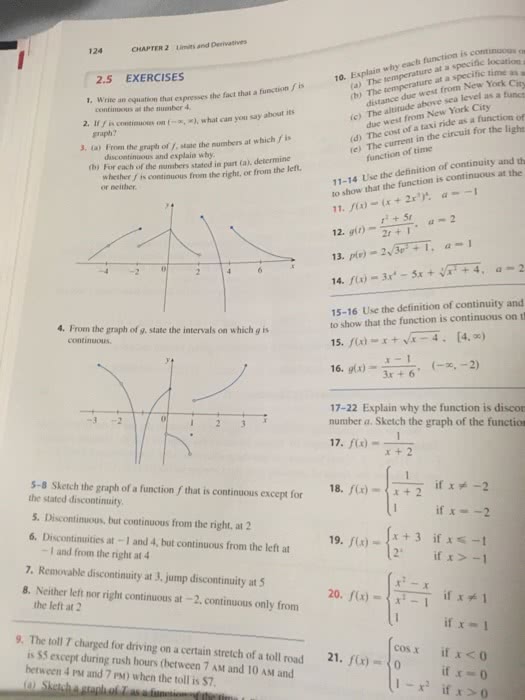
124 CHAPTER 2 Limits and Derivatives that a function fis 10. Explain why each function is continous The temperature at a specific location 2.5 EXERCISES ific location a (b) The temperature at a specific time due west from New York City (e) The current in the circuit for the li fic time as distance due west from New York (c) The altitude above sea level as (a) an equation that expresses the fact that a function f is 1. Write continoous at the number 4. level as a funct 2 If f is continuous on (, »«), what can you say about its 3. (a) From the graph of f, state the numbers at which f is graph? i ride as a function of (d) The cost of a taxi discontinuous and explain why (b) For each of the numbers stated in part (a), determine function of time 11-14 Use the definition of continuity 11. x) -( +2x a 12.9(,) , a-2 whether f is continuous from the right, or from the left. or neither and th to show that the function is continuous at the + 5 2t + 1 a-2 14.f(x)ä¸3r' _ 5x + :/r-4, 15-16 Use the definition of continuity and to show that the function is continuous on t 4. From the graph of g. state the intervals on which g is continuoS 16. g(x)(oc,-2) 3x + 6 17-22 Explain why the function is discon number a. Sketch the graph of the functios 17. f) +2 5-8 Sketch the graph of a function f that is continuous except for the stated discontinuity 5. Discontinuous, but continuous from the right, at2 6. Discontinuities at -1 and 4, but continuous from the left at 18, f(x)-{x + 2 if x 2 u from o le i19.1). 3i1 -I and from the right at 4 7. Removable discontinuity at 3, jump discontinuity at 5 8. Neither left nor right continuous at -2, continuous only from the left at 2 20. fx)x- 9. The toll T charged for driving on a certain stretch of a toll road 21. )-if x is $5 except during rush hours (between 7 AM and 10 AM and between 4 PM and 7 PM) when the toll is $7 cosx if x0
Show transcribed image text 124 CHAPTER 2 Limits and Derivatives that a function fis 10. Explain why each function is continous The temperature at a specific location 2.5 EXERCISES ific location a (b) The temperature at a specific time due west from New York City (e) The current in the circuit for the li fic time as distance due west from New York (c) The altitude above sea level as (a) an equation that expresses the fact that a function f is 1. Write continoous at the number 4. level as a funct 2 If f is continuous on (, »«), what can you say about its 3. (a) From the graph of f, state the numbers at which f is graph? i ride as a function of (d) The cost of a taxi discontinuous and explain why (b) For each of the numbers stated in part (a), determine function of time 11-14 Use the definition of continuity 11. x) -( +2x a 12.9(,) , a-2 whether f is continuous from the right, or from the left. or neither and th to show that the function is continuous at the + 5 2t + 1 a-2 14.f(x)ä¸3r' _ 5x + :/r-4, 15-16 Use the definition of continuity and to show that the function is continuous on t 4. From the graph of g. state the intervals on which g is continuoS 16. g(x)(oc,-2) 3x + 6 17-22 Explain why the function is discon number a. Sketch the graph of the functios 17. f) +2 5-8 Sketch the graph of a function f that is continuous except for the stated discontinuity 5. Discontinuous, but continuous from the right, at2 6. Discontinuities at -1 and 4, but continuous from the left at 18, f(x)-{x + 2 if x 2 u from o le i19.1). 3i1 -I and from the right at 4 7. Removable discontinuity at 3, jump discontinuity at 5 8. Neither left nor right continuous at -2, continuous only from the left at 2 20. fx)x- 9. The toll T charged for driving on a certain stretch of a toll road 21. )-if x is $5 except during rush hours (between 7 AM and 10 AM and between 4 PM and 7 PM) when the toll is $7 cosx if x0