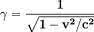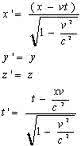Introduction. Telescope time is a valuablecommodity in astronomy, so astronomers plan their observationscarefully. One of the first steps is to choose what type ofobservation to make. Recall that three basic types of astronomicalobservation are imaging (taking a photograph of anobject), spectroscopy (spreading an object's light into aspectrum), and timing (measuring how an object's lightvaries with time).
Part A: Sort each of the astronomical questionsbelow into the appropriate bin based on the type of observation youwould need to perform to answer it.
Three Categories: Imagine, Spectroscopy andTiming
The Questions:
1. "What are the major surface features of Mars?"
2. "What is the temperature of Jupiter's atmosphere?"
3. "Does the star Mira vary in brightness?"
4. "How large is the Andromeda Galaxy?"
5. "What is the chemical composition of the Crab Nebula?"
6. "Is the X-ray emission fro the galactic center steady orchanging?"
7. "Is the star Vega moving toward us or away from us?"
8. "Are stars in the Orion Nebula surrounded by dusty disks ofgas?"
------------------------
Introduction: Different telescopes areoptimized for observing different wavelengths of light, so anotherconsideration in planning an observation is deciding what type oftelescope to use.
Part B: Each of the following statementsdescribes an astronomical measurement. Place each measurement intothe appropriate bin based on the type of telescope you would use tomake it.
Three Categories: Infrared Telescope, VisibleLight Telescope and X-Ray Telescope
The Statements:
1. Study a dense cloud of cold gas in space.
2. Measure the brightness of a star that is similar to ourSun.
3. Observe the hot (1-million K) gas in the Sun's corona.
4. Obtain a spectrum of sunlight reflected by Mars.
5. Determine the surface temperature of Venus.
6. Look for high-energy radiation from a supernova.
Thank you so much to whoever helps!