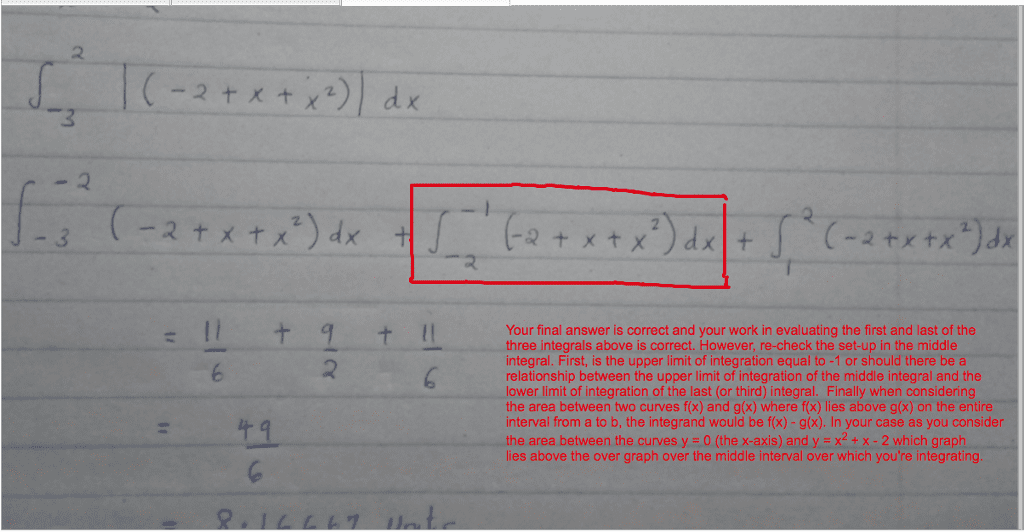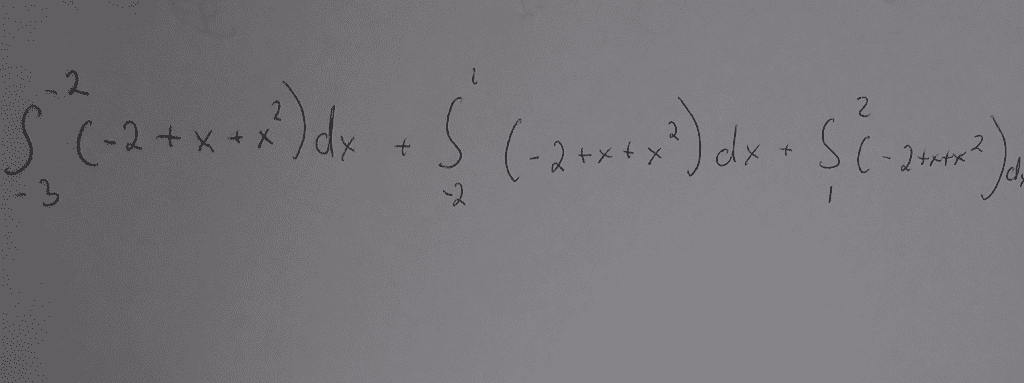MAT136H1 Lecture Notes - Integral


92
MAT136H1 Full Course Notes
Verified Note
92 documents
Document Summary
Question #2 (easy): expressing the limit as the definite integral. By the definition of the definite integral, the limit expression is set equal to the definite integral over the interval [ ] ( ) is integrable on [ ]. Therefore, direct correlation between the limit and definite integral is established: ) , where and and: definite integral means the interval [ ]is fixed. Definite integral describes this as ( : from the limit becomes in the integral since . ) ( ) in the limit becomes general function notation ( ) in the integral. Convert the limit into a definite integral over the given interval. Solution: the interval is set as [ ], thus .